We use the structure lattice, introduced in Part I, to undertake a systematic study of the class $\mathscr{S}$ consisting of compactly generated, topologically simple, totally disconnected locally compact groups that are nondiscrete. Given $G\in \mathscr{S}$ , we show that compact open subgroups of $G$ involve finitely many isomorphism types of composition factors, and do not have any soluble normal subgroup other than the trivial one. By results of Part I, this implies that the centralizer lattice and local decomposition lattice of $G$ are Boolean algebras. We show that the $G$ -action on the Stone space of those Boolean algebras is minimal, strongly proximal, and microsupported. Building upon those results, we obtain partial answers to the following key problems: Are all groups in $\mathscr{S}$ abstractly simple? Can a group in $\mathscr{S}$ be amenable? Can a group in $\mathscr{S}$ be such that the contraction groups of all of its elements are trivial?

Let $G$ be a totally disconnected, locally compact group. A closed subgroup of $G$ is locally normal if its normalizer is open in $G$ . We begin an investigation of the structure of the family of closed locally normal subgroups of $G$ . Modulo commensurability, this family forms a modular lattice ${\mathcal{L}}{\mathcal{N}}(G)$ , called the structure lattice of $G$ . We show that $G$ admits a canonical maximal quotient $H$ for which the quasicentre and the abelian locally normal subgroups are trivial. In this situation ${\mathcal{L}}{\mathcal{N}}(H)$ has a canonical subset called the centralizer lattice, forming a Boolean algebra whose elements correspond to centralizers of locally normal subgroups. If $H$ is second-countable and acts faithfully on its centralizer lattice, we show that the topology of $H$ is determined by its algebraic structure (and thus invariant by every abstract group automorphism), and also that the action on the Stone space of the centralizer lattice is universal for a class of actions on profinite spaces. Most of the material is developed in the more general framework of Hecke pairs.

We generalize Brooks’ theorem to show that if $G$ is a Borel graph on a standard Borel space $X$ of degree bounded by $d\geqslant 3$ which contains no $(d+1)$ -cliques, then $G$ admits a ${\it\mu}$ -measurable $d$ -coloring with respect to any Borel probability measure ${\it\mu}$ on $X$ , and a Baire measurable $d$ -coloring with respect to any compatible Polish topology on $X$ . The proof of this theorem uses a new technique for constructing one-ended spanning subforests of Borel graphs, as well as ideas from the study of list colorings. We apply the theorem to graphs arising from group actions to obtain factor of IID $d$ -colorings of Cayley graphs of degree $d$ , except in two exceptional cases.

A locally compact group G is compact if and only if its convolution algebras contain non-zero (weakly) completely continuous elements. Dually, G is discrete if its function algebras contain non-zero completely continuous elements. We prove non-commutative versions of these results in the case of locally compact quantum groups.

We give a means of estimating the equivariant compression of a group G in terms of properties of open subgroups G i ⊂ G whose direct limit is G. Quantifying a result by Gal, we also study the behaviour of the equivariant compression under amalgamated free products G 1∗H G 2 where H is of finite index in both G 1 and G 2.

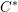This paper is about the reduced group $C^{\ast }$-algebras of real redu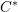ctive groups, and about Hilbert $C^{\ast }$-modules over these $C^{\ast }$-algebras. We shall do three things. First, we shall apply theorems from the tempered representation theory of reductive groups to determine the structure of the reduced $C^{\ast }$-algebra (the result has been known for some time, but it is difficult to assemble a full treatment from the existing literature). Second, we shall use the structure of the reduced $C^{\ast }$-algebra to determine the structure of the Hilbert $C^{\ast }$-bimodule that represents the functor of parabolic induction. Third, we shall prove that the parabolic induction bimodule admits a secondary inner product, using which we can define a functor of parabolic restriction in tempered representation theory. We shall prove in a sequel to this paper that parabolic restriction is adjoint, on both the left and the right, to parabolic induction in the context of tempered unitary Hilbert space representations.

Let $\text{H}$ be a subgroup of some locally compact group $\text{G}$. Assume that $\text{H}$ is approximable by discrete subgroups and that $\text{G}$ admits neighborhood bases which are almost invariant under conjugation by finite subsets of $\text{H}$. Let $m:\text{G}\rightarrow \mathbb{C}$ be a bounded continuous symbol giving rise to an $L_{p}$-bounded Fourier multiplier (not necessarily completely bounded) on the group von Neumann algebra of $\text{G}$ for some $1\leqslant p\leqslant \infty$. Then, $m_{\mid _{\text{H}}}$ yields an $L_{p}$-bounded Fourier multiplier on the group von Neumann algebra of $\text{H}$ provided that the modular function ${\rm\Delta}_{\text{G}}$ is equal to 1 over $\text{H}$. This is a noncommutative form of de Leeuw’s restriction theorem for a large class of pairs $(\text{G},\text{H})$. Our assumptions on $\text{H}$ are quite natural, and they recover the classical result. The main difference with de Leeuw’s original proof is that we replace dilations of Gaussians by other approximations of the identity for which certain new estimates on almost-multiplicative maps are crucial. Compactification via lattice approximation and periodization theorems are also investigated.

We prove that if ${\it\rho}$ is an irreducible positive definite function in the Fourier–Stieltjes algebra $B(G)$ of a locally compact group $G$ with $\Vert {\it\rho}\Vert _{B(G)}=1$, then the iterated powers $({\it\rho}^{n})$ as a sequence of unital completely positive maps on the group $C^{\ast }$-algebra converge to zero in the strong operator topology.

Hughes has defined a class of groups that we call finite similarity structure (FSS) groups. Each FSS group acts on a compact ultrametric space by local similarities. The best-known example is Thompson’s group V. Guided by previous work on Thompson’s group, we show that many FSS groups are of type F∞. This generalizes work of Ken Brown from the 1980s.

Let G be a finitely generated group with polynomial growth, and let ω be a weight, i.e. a sub-multiplicative function on G with positive values. We study when the weighted group algebra ℓ1 (G, ω) is isomorphic to an operator algebra. We show that ℓ1 (G, ω) is isomorphic to an operator algebra if ω is a polynomial weight with large enough degree or an exponential weight of order 0 < α < 1. We demonstrate that the order of growth of G plays an important role in this problem. Moreover, the algebraic centre of ℓ1 (G, ω) is isomorphic to a Q-algebra, and hence satisfies a multi-variable von Neumann inequality. We also present a more detailed study of our results when G consists of the d-dimensional integers ℤd or the three-dimensional discrete Heisenberg group ℍ3(ℤ). The case of the free group with two generators is considered as a counter-example of groups with exponential growth.

An algebra A is said to be directly finite if each left-invertible element in the (conditional) unitization of A is right invertible. We show that the reduced group C*-algebra of a unimodular group is directly finite, extending known results for the discrete case. We also investigate the corresponding problem for algebras of p-pseudofunctions, showing that these algebras are directly finite if G is amenable and unimodular, or unimodular with the Kunze–Stein property. An exposition is also given of how existing results from the literature imply that L1(G) is not directly finite when G is the affine group of either the real or complex line.

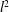In this note we show that the members of a certain class of local similarity groups are ${l}^{2}$-invisible, i.e. the (non-reduced) group homology of the regular unitary representation vanishes in all degrees. This class contains groups of type ${F}_{\infty }$, e.g. Thompson’s group $V$ and Nekrashevych–Röver groups. They yield counterexamples to a generalized zero-in-the-spectrum conjecture for groups of type ${F}_{\infty }$.

It is well known that a finitely generated group ${\rm\Gamma}$ has Kazhdan’s property (T) if and only if the Laplacian element ${\rm\Delta}$ in $\mathbb{R}[{\rm\Gamma}]$ has a spectral gap. In this paper, we prove that this phenomenon is witnessed in $\mathbb{R}[{\rm\Gamma}]$. Namely, ${\rm\Gamma}$ has property (T) if and only if there exist a constant ${\it\kappa}>0$ and a finite sequence ${\it\xi}_{1},\ldots ,{\it\xi}_{n}$ in $\mathbb{R}[{\rm\Gamma}]$ such that ${\rm\Delta}^{2}-{\it\kappa}{\rm\Delta}=\sum _{i}{\it\xi}_{i}^{\ast }{\it\xi}_{i}$. This result suggests the possibility of finding new examples of property (T) groups by solving equations in $\mathbb{R}[{\rm\Gamma}]$, possibly with the assistance of computers.

We study the affine formal algebra $R$ of the Lubin–Tate deformation space as a module over two different rings. One is the completed group ring of the automorphism group $\Gamma $ of the formal module of the deformation problem, the other one is the spherical Hecke algebra of a general linear group. In the most basic case of height two and ground field $\mathbb {Q}_p$, our structure results include a flatness assertion for $R$ over the spherical Hecke algebra and allow us to compute the continuous (co)homology of $\Gamma $ with coefficients in $R$.

The notion of BSE algebras was introduced and first studied by Takahasi and Hatori and later studied by Kaniuth and Ülger. This notion depends strongly on the multiplier algebra $M( \mathcal{A} )$ of a commutative Banach algebra $ \mathcal{A} $. In this paper we first present a characterisation of the multiplier algebra of the direct sum of two commutative semisimple Banach algebras. Then as an application we show that $ \mathcal{A} \oplus \mathcal{B} $ is a BSE algebra if and only if $ \mathcal{A} $ and $ \mathcal{B} $ are BSE. We also prove that if the algebra $ \mathcal{A} \hspace{0.167em} {\mathop{\times }\nolimits}_{\theta } \hspace{0.167em} \mathcal{B} $ with $\theta $-Lau product is a BSE algebra and $ \mathcal{B} $ is unital then $ \mathcal{B} $ is a BSE algebra. We present some examples which show that the BSE property of $ \mathcal{A} \hspace{0.167em} {\mathop{\times }\nolimits}_{\theta } \hspace{0.167em} \mathcal{B} $ does not imply the BSE property of $ \mathcal{A} $, even in the case where $ \mathcal{B} $ is unital.

Higher-rank graphs were introduced by Kumjian and Pask to provide models for higher-rank Cuntz–Krieger algebras. In a previous paper, we constructed 2-graphs whose path spaces are rank-two subshifts of finite type, and showed that this construction yields aperiodic 2-graphs whoseC*-algebras are simple and are not ordinary graph algebras. Here we show that the construction also gives a family of periodic 2-graphs which we call domino graphs. We investigate the combinatorial structure of domino graphs, finding interesting points of contact with the existing combinatorial literature, and prove a structure theorem for the C*-algebras of domino graphs.

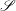
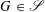
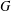
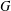
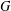
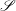
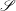
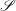
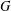
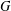
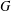
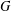
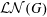
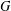
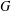
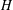
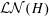
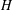
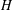
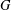
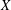
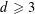
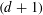
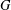
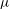
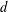
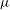
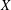
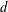
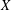
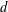
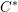
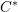
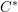
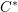
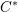
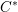
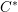
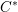
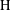
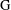
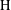
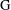
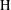
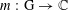
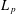
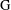
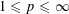
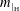
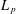
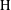
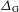
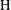
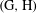
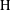
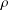
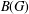
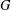
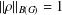
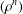
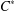
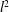
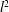
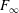
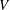
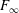
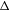
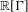
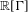
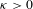
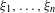
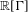
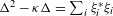
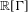
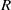
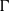
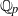
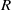
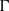
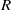
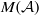
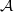
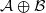
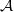
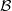
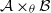
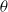
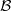
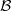
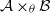
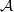
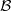
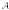We study when certain properties of Banach algebras are stable under ultrapower constructions. In particular, we consider when every ultrapower of is Arens regular, and give some evidence that this is so if and only if is isomorphic to a closed subalgebra of operators on a super-reflexive Banach space. We show that such ideas are closely related to whether one can sensibly define an ultrapower of a dual Banach algebraffi We study how tensor products of ultrapowers behave, and apply this to study the question of when every ultrapower of is amenable. We provide an abstract characterization in terms of something like an approximate diagonal, and consider when every ultrapower of a C*-algebra, or a group L1-convolution algebra, is amenable.

It is shown that for the computation of the Kazhdan constant for a compact group only the regular representation restricted to the orthogonal complement of the constant functions needs to be taken into account.

Let a1… ad be a basis of the Lie algebra g of a connected Lie group G and let M be a Lie subgroup of,G. If dx is a non-zero positive quasi-invariant regular Borel measure on the homogeneous space X = G/M and S: X × G → C is a continuous cocycle, then under a rather weak condition on dx and S there exists in a natural way a (weakly*) continuous representation U of G in Lp (X;dx) for all p ε [1,].

Let Ai be the infinitesimal generator with respect to U and the direction ai, for all i ∈ { 1… d}. We consider n–th order strongly elliptic operators H = ΣcαAα with complex coefficients cα. We show that the semigroup S generated by the closure of H has a reduced heat kernel K and we derive upper bounds for k and all its derivatives.

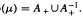Let Γ be a free noncommutative group with free generating set A+. Let μ ∈ ℓ1(Γ) be real, symmetric, nonnegative and suppose that supp. Let λ be an endpoint of the spectrum of μ considered as a convolver on ℓ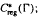2(Γ). Then λ − μ is in the left kernel of exactly one pure state of the reduced in particular, Paschke's conjecture holds for λ − μ.