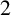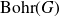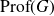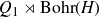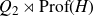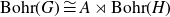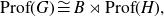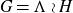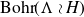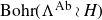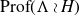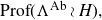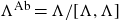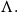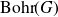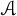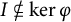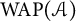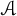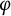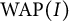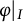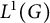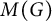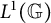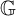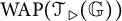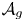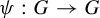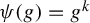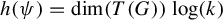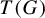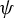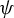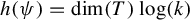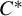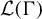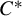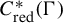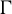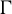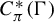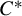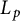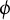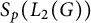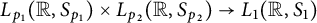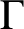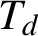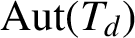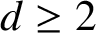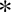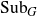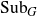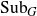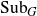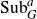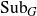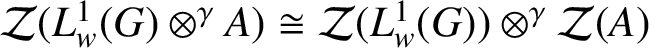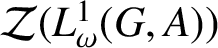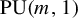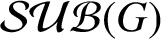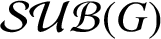Refine listing
Actions for selected content:
97 results in 22Dxx
Approximate homomorphisms and sofic approximations of orbit equivalence relations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 12 / December 2024
- Published online by Cambridge University Press:
- 15 March 2024, pp. 3455-3480
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RADU GROUPS ACTING ON TREES ARE CCR
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 06 March 2024, pp. 149-186
- Print publication:
- October 2024
-
- Article
- Export citation
Arens regularity of ideals of the group algebra of a compact Abelian group
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 27 October 2023, pp. 718-734
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Exponential multiple mixing for commuting automorphisms of a nilmanifold
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 7 / July 2024
- Published online by Cambridge University Press:
- 11 October 2023, pp. 1729-1740
- Print publication:
- July 2024
-
- Article
- Export citation
On Bohr compactifications and profinite completions of group extensions
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 09 October 2023, pp. 373-393
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Invariant means on weakly almost periodic functionals with application to quantum groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 16 January 2023, pp. 927-936
- Print publication:
- September 2023
-
- Article
- Export citation
Equidistribution of Hodge loci II
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 12 January 2023, pp. 1-52
- Print publication:
- January 2023
-
- Article
- Export citation
The topological entropy of powers on Lie groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 11 / November 2023
- Published online by Cambridge University Press:
- 13 December 2022, pp. 3726-3744
- Print publication:
- November 2023
-
- Article
- Export citation
On invariant subalgebras of group
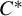 $C^*$ and von Neumann algebras
$C^*$ and von Neumann algebras
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 10 / October 2023
- Published online by Cambridge University Press:
- 04 November 2022, pp. 3341-3353
- Print publication:
- October 2023
-
- Article
- Export citation
Multilinear transference of Fourier and Schur multipliers acting on noncommutative
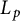 $L_p$-spaces
$L_p$-spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 03 November 2022, pp. 1986-2006
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GROUPS ACTING ON TREES WITH PRESCRIBED LOCAL ACTION
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 115 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 12 September 2022, pp. 240-288
- Print publication:
- October 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CAYLEY–ABELS GRAPHS AND INVARIANTS OF TOTALLY DISCONNECTED, LOCALLY COMPACT GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 114 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 13 April 2022, pp. 145-177
- Print publication:
- April 2023
-
- Article
- Export citation
C
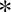 $^{\ast }$-simplicity has no local obstruction
$^{\ast }$-simplicity has no local obstruction
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 16 March 2022, e18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Distal Actions of Automorphisms of Lie Groups G on SubG
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 2 / September 2022
- Published online by Cambridge University Press:
- 21 December 2021, pp. 457-478
- Print publication:
- September 2022
-
- Article
- Export citation
CENTRE OF BANACH ALGEBRA VALUED BEURLING ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 13 September 2021, pp. 490-498
- Print publication:
- June 2022
-
- Article
- Export citation
Multiplicative constants and maximal measurable cocycles in bounded cohomology
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 11 / November 2022
- Published online by Cambridge University Press:
- 31 August 2021, pp. 3490-3525
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Harmonic models and Bernoullicity
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 19 August 2021, pp. 2160-2198
- Print publication:
- October 2021
-
- Article
- Export citation
ON THE CONNECTEDNESS OF THE CHABAUTY SPACE OF A LOCALLY COMPACT PRONILPOTENT GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 17 May 2021, pp. 161-170
- Print publication:
- February 2022
-
- Article
- Export citation
On Polish groups admitting non-essentially countable actions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 29 December 2020, pp. 180-194
- Print publication:
- January 2022
-
- Article
-
- You have access
- Open access
- Export citation
DISTAL ACTIONS OF AUTOMORPHISMS OF NILPOTENT GROUPS G ON SUBG AND APPLICATIONS TO LATTICES IN LIE GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 23 June 2020, pp. 343-362
- Print publication:
- May 2021
-
- Article
- Export citation