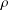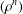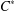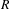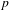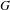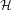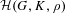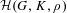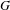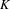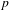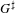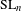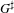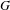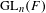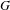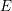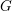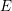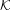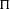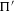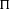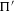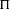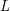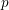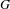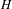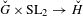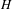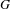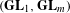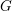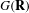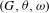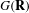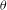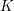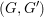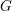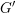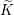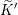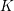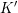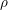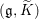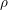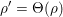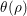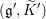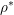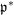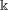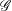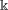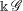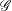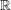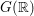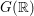Refine listing
Actions for selected content:
543 results in 22xxx
A NOTE ON PSEUDOVARIETIES OF COMPLETELY REGULAR SEMIGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 16 June 2015, pp. 233-237
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation
ON ITERATED POWERS OF POSITIVE DEFINITE FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 16 June 2015, pp. 440-443
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
THE PRO-p-IWAHORI HECKE ALGEBRA OF A REDUCTIVE p-ADIC GROUP III (SPHERICAL HECKE ALGEBRAS AND SUPERSINGULAR MODULES)
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 16 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 03 June 2015, pp. 571-608
- Print publication:
- June 2017
-
- Article
- Export citation
HECKE ALGEBRAS FOR INNER FORMS OF
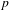 $p$ -ADIC SPECIAL LINEAR GROUPS
$p$ -ADIC SPECIAL LINEAR GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 16 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 05 May 2015, pp. 351-419
- Print publication:
- April 2017
-
- Article
- Export citation
Finiteness Properties of Some Groups of Local Similarities
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 10 April 2015, pp. 379-402
-
- Article
-
- You have access
- Export citation
Elliptic Springer theory
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 8 / August 2015
- Published online by Cambridge University Press:
- 08 April 2015, pp. 1568-1584
- Print publication:
- August 2015
-
- Article
- Export citation
WHITTAKER PERIODS, MOTIVIC PERIODS, AND SPECIAL VALUES OF TENSOR PRODUCT
 $L$ -FUNCTIONS
$L$ -FUNCTIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 4 / October 2016
- Published online by Cambridge University Press:
- 31 March 2015, pp. 711-769
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
Endoscopie et conjecture locale raffinée de Gan–Gross–Prasad pour les groupes unitaires
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 7 / July 2015
- Published online by Cambridge University Press:
- 18 February 2015, pp. 1309-1371
- Print publication:
- July 2015
-
- Article
- Export citation
GEOMETRIC TAMELY RAMIFIED LOCAL THETA CORRESPONDENCE IN THE FRAMEWORK OF THE GEOMETRIC LANGLANDS PROGRAM
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 3 / July 2016
- Published online by Cambridge University Press:
- 18 February 2015, pp. 625-671
- Print publication:
- July 2016
-
- Article
- Export citation
Diophantine properties of nilpotent Lie groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 6 / June 2015
- Published online by Cambridge University Press:
- 13 January 2015, pp. 1157-1188
- Print publication:
- June 2015
-
- Article
- Export citation
Some Weighted Group Algebras are Operator Algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 05 January 2015, pp. 499-519
-
- Article
-
- You have access
- Export citation
LINEAR AND PROJECTIVE BOUNDARY OF NILPOTENT GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 22 December 2014, pp. 591-632
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
KILLING FRAMES AND S-CURVATURE OF HOMOGENEOUS FINSLER SPACES*
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 2 / May 2015
- Published online by Cambridge University Press:
- 22 December 2014, pp. 457-464
- Print publication:
- May 2015
-
- Article
-
- You have access
- Export citation
META-CENTRALIZERS OF NON-LOCALLY COMPACT GROUP ALGEBRAS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 2 / May 2015
- Published online by Cambridge University Press:
- 18 December 2014, pp. 349-364
- Print publication:
- May 2015
-
- Article
-
- You have access
- Export citation
TEMPERED SPECTRAL TRANSFER IN THE TWISTED ENDOSCOPY OF REAL GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 3 / July 2016
- Published online by Cambridge University Press:
- 17 December 2014, pp. 569-612
- Print publication:
- July 2016
-
- Article
- Export citation
DIRECTLY FINITE ALGEBRAS OF PSEUDOFUNCTIONS ON LOCALLY COMPACT GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 17 December 2014, pp. 693-707
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
A study of the representations supported by the orbit closure of the determinant
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 2 / February 2015
- Published online by Cambridge University Press:
- 24 October 2014, pp. 292-312
- Print publication:
- February 2015
-
- Article
- Export citation
Invariants and
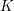 $K$-spectrums of local theta lifts
$K$-spectrums of local theta lifts
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 17 September 2014, pp. 179-206
- Print publication:
- January 2015
-
- Article
- Export citation
MODULES OVER ÉTALE GROUPOID ALGEBRAS AS SHEAVES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 09 September 2014, pp. 418-429
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
The real Chevalley involution
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 12 / December 2014
- Published online by Cambridge University Press:
- 27 August 2014, pp. 2127-2142
- Print publication:
- December 2014
-
- Article
- Export citation