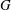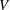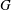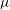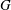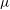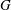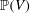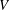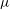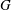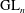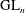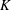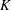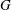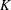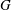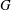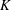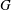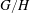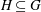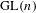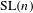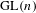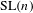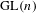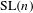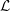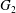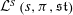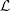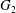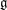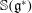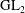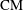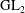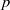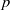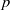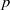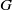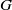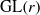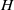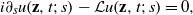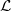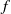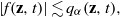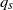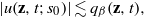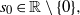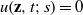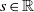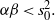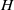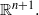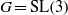Refine listing
Actions for selected content:
543 results in 22xxx
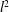 ${l}^{2}$-invisibility and a class of local similarity groups
${l}^{2}$-invisibility and a class of local similarity groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 10 / October 2014
- Published online by Cambridge University Press:
- 19 August 2014, pp. 1742-1754
- Print publication:
- October 2014
-
- Article
- Export citation
EXTENSIONS ENTRE SÉRIES PRINCIPALES
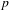 $p$-ADIQUES ET MODULO
$p$-ADIQUES ET MODULO 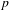 $p$ DE
$p$ DE 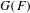 $G(F)$
$G(F)$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 08 August 2014, pp. 225-270
- Print publication:
- April 2016
-
- Article
- Export citation
SUR LE COMPTAGE DES FIBRÉS DE HITCHIN NILPOTENTS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 07 August 2014, pp. 91-164
- Print publication:
- January 2016
-
- Article
-
- You have access
- Export citation
NONCOMMUTATIVE REAL ALGEBRAIC GEOMETRY OF KAZHDAN’S PROPERTY (T)
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 30 July 2014, pp. 85-90
- Print publication:
- January 2016
-
- Article
- Export citation
Reduction of Homogeneous Riemannian Structures
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 18 July 2014, pp. 81-106
-
- Article
-
- You have access
- Export citation
Random walks on projective spaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 9 / September 2014
- Published online by Cambridge University Press:
- 17 July 2014, pp. 1579-1606
- Print publication:
- September 2014
-
- Article
- Export citation
Raising the level for
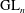 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\text {GL}_{{n}}$
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\text {GL}_{{n}}$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 2 / 01 July 2014
- Published online by Cambridge University Press:
- 10 June 2014, e16
-
- Article
-
- You have access
- Open access
- Export citation
SUPERBOSONIZATION VIA RIESZ SUPERDISTRIBUTIONS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 2 / 01 July 2014
- Published online by Cambridge University Press:
- 14 May 2014, e9
-
- Article
-
- You have access
- Open access
- Export citation
A NOTE ON
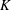 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}K$-SPACES
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}K$-SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 12 May 2014, pp. 144-148
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
The elliptic Weyl character formula
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 7 / July 2014
- Published online by Cambridge University Press:
- 12 May 2014, pp. 1196-1234
- Print publication:
- July 2014
-
- Article
- Export citation
LIMIT MULTIPLICITIES FOR PRINCIPAL CONGRUENCE SUBGROUPS OF
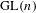 $\text{GL}(n)$ AND
$\text{GL}(n)$ AND 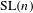 $\text{SL}(n)$
$\text{SL}(n)$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 14 / Issue 3 / July 2015
- Published online by Cambridge University Press:
- 08 May 2014, pp. 589-638
- Print publication:
- July 2015
-
- Article
- Export citation
The Rankin–Selberg integral with a non-unique model for the standard
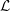 $\mathcal{L}$ -function of
$\mathcal{L}$ -function of 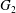 $G_2$
$G_2$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 14 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 08 May 2014, pp. 149-184
- Print publication:
- January 2015
-
- Article
- Export citation
Deformations of the Lie–Poisson sphere of a compact semisimple Lie algebra
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 4 / April 2014
- Published online by Cambridge University Press:
- 27 March 2014, pp. 568-578
- Print publication:
- April 2014
-
- Article
- Export citation
On the homomorphisms between scalar generalized Verma modules
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 5 / May 2014
- Published online by Cambridge University Press:
- 26 March 2014, pp. 877-892
- Print publication:
- May 2014
-
- Article
- Export citation
Galois representations attached to automorphic forms on
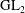 ${\rm GL}_2$ over
${\rm GL}_2$ over 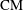 ${\rm CM}$ fields
${\rm CM}$ fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 4 / April 2014
- Published online by Cambridge University Press:
- 26 March 2014, pp. 523-567
- Print publication:
- April 2014
-
- Article
- Export citation
Cartan subgroups of groups definable ino-minimal structures
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 4 / October 2014
- Published online by Cambridge University Press:
- 28 November 2013, pp. 849-893
- Print publication:
- October 2014
-
- Article
- Export citation
On a classification of irreducible admissible modulo
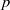 $p$ representations of a
$p$ representations of a 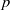 $p$-adic split reductive group
$p$-adic split reductive group
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 12 / December 2013
- Published online by Cambridge University Press:
- 09 October 2013, pp. 2139-2168
- Print publication:
- December 2013
-
- Article
- Export citation
Comptage des
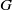 $G$-chtoucas: la partie elliptique
$G$-chtoucas: la partie elliptique
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 12 / December 2013
- Published online by Cambridge University Press:
- 07 October 2013, pp. 2169-2183
- Print publication:
- December 2013
-
- Article
- Export citation
UNIQUENESS OF SOLUTIONS TO SCHRÖDINGER EQUATIONS ON
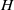 $H$-TYPE GROUPS
$H$-TYPE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 95 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 07 August 2013, pp. 297-314
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
Buildings, spiders, and geometric Satake
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 11 / November 2013
- Published online by Cambridge University Press:
- 10 July 2013, pp. 1871-1912
- Print publication:
- November 2013
-
- Article
- Export citation
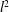
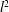
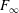
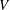
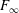
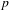
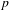
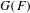
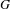

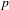
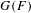
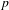
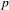

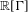

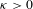
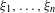
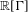
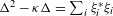
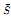 . The situation when
. The situation when