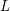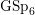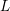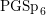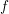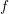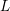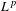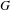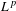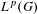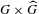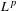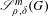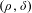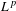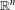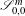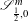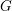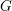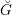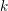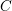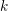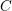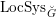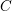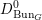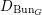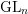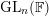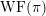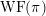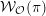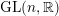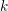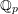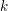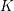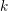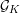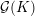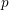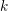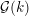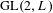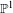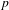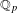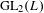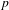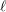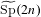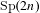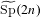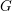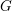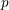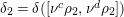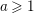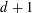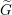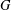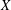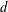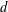Refine listing
Actions for selected content:
543 results in 22xxx
The spin
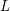 $L$ -function on
$L$ -function on 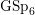 $\text{GSp}_{6}$ for Siegel modular forms
$\text{GSp}_{6}$ for Siegel modular forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 7 / July 2017
- Published online by Cambridge University Press:
- 10 May 2017, pp. 1391-1432
- Print publication:
- July 2017
-
- Article
- Export citation
ARITHMÉTICITÉ DE SOUS-GROUPES D’UN PRODUIT DE GROUPES DE RANG
 $1$
$1$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 10 April 2017, pp. 225-248
- Print publication:
- January 2019
-
- Article
- Export citation
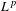 $L^{p}$-BOUNDS FOR PSEUDO-DIFFERENTIAL OPERATORS ON COMPACT LIE GROUPS
$L^{p}$-BOUNDS FOR PSEUDO-DIFFERENTIAL OPERATORS ON COMPACT LIE GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 3 / May 2019
- Published online by Cambridge University Press:
- 03 April 2017, pp. 531-559
- Print publication:
- May 2019
-
- Article
-
- You have access
- Open access
- Export citation
Geometric Langlands in prime characteristic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 2 / February 2017
- Published online by Cambridge University Press:
- 16 February 2017, pp. 395-452
- Print publication:
- February 2017
-
- Article
- Export citation
Generalized and degenerate Whittaker models
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 2 / February 2017
- Published online by Cambridge University Press:
- 06 February 2017, pp. 223-256
- Print publication:
- February 2017
-
- Article
- Export citation
Stable vectors in Moy–Prasad filtrations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 2 / February 2017
- Published online by Cambridge University Press:
- 09 February 2017, pp. 358-372
- Print publication:
- February 2017
-
- Article
- Export citation
LOCALLY ANALYTIC REPRESENTATIONS OF
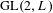 $\text{GL}(2,L)$ VIA SEMISTABLE MODELS OF
$\text{GL}(2,L)$ VIA SEMISTABLE MODELS OF 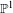 $\mathbb{P}^{1}$
$\mathbb{P}^{1}$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 12 January 2017, pp. 125-187
- Print publication:
- January 2019
-
- Article
- Export citation
Corrigendum: Analytic representation theory of Lie groups: general theory and analytic globalizations of Harish-Chandra modules
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 19 January 2017, pp. 214-217
- Print publication:
- January 2017
-
- Article
-
- You have access
- HTML
- Export citation
A formula for certain Shalika germs of ramified unitary groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 19 January 2017, pp. 175-213
- Print publication:
- January 2017
-
- Article
- Export citation
SPECTRAL TRANSFER FOR METAPLECTIC GROUPS. I. LOCAL CHARACTER RELATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 07 December 2016, pp. 25-123
- Print publication:
- January 2019
-
- Article
- Export citation
The affine Grassmannian and the Springer resolution in positive characteristic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 12 / December 2016
- Published online by Cambridge University Press:
- 28 November 2016, pp. 2627-2677
- Print publication:
- December 2016
-
- Article
- Export citation
MOVING FRAMES AND NOETHER’S CONSERVATION LAWS—THE GENERAL CASE
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 25 October 2016, e29
-
- Article
-
- You have access
- Open access
- Export citation
HARDY AND MIYACHI THEOREMS FOR HEISENBERG MOTION GROUPS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 229 / March 2018
- Published online by Cambridge University Press:
- 20 October 2016, pp. 1-20
- Print publication:
- March 2018
-
- Article
-
- You have access
- HTML
- Export citation
ON VARIETIES OF ABELIAN TOPOLOGICAL GROUPS WITH COPRODUCTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 19 October 2016, pp. 54-65
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
COMPOSITION FACTORS OF A CLASS OF INDUCED REPRESENTATIONS OF CLASSICAL
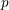 $p$ -ADIC GROUPS
$p$ -ADIC GROUPS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 227 / September 2017
- Published online by Cambridge University Press:
- 18 October 2016, pp. 16-48
- Print publication:
- September 2017
-
- Article
-
- You have access
- HTML
- Export citation
KŐNIG’S LINE COLORING AND VIZING’S THEOREMS FOR GRAPHINGS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 19 September 2016, e27
-
- Article
-
- You have access
- Open access
- Export citation
On a lifting problem of L-packets
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 9 / September 2016
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1800-1850
- Print publication:
- September 2016
-
- Article
- Export citation
BROOKS’ THEOREM FOR MEASURABLE COLORINGS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 24 June 2016, e16
-
- Article
-
- You have access
- Open access
- Export citation
Adjoint Orbits of Semi-Simple Lie Groups and Lagrangian Submanifolds
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 15 June 2016, pp. 361-385
-
- Article
- Export citation
COMPACT ELEMENTS AND OPERATORS OF QUANTUM GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 445-462
- Print publication:
- May 2017
-
- Article
-
- You have access
- Export citation