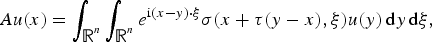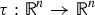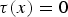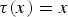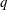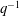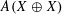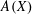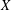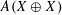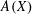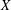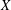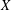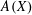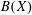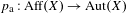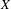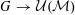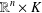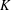Refine listing
Actions for selected content:
543 results in 22xxx
Pseudo-differential operators with nonlinear quantizing functions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 23 January 2019, pp. 103-130
- Print publication:
- February 2020
-
- Article
-
- You have access
- Open access
- Export citation
Lipschitz 1-connectedness for Some Solvable Lie Groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 533-555
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
Eisenstein Series Arising from Jordan Algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 09 January 2019, pp. 183-201
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
Models of Representations and Langlands Functoriality
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 07 January 2019, pp. 676-707
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
Completeness of Infinite-dimensional Lie Groups in Their Left Uniformity
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 131-152
- Print publication:
- February 2019
-
- Article
-
- You have access
- Open access
- Export citation
Casselman’s Basis of Iwahori Vectors and Kazhdan–Lusztig Polynomials
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 1351-1366
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
Actions of Semitopological Groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 04 January 2019, pp. 441-450
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
Finsler Warped Product Metrics of Douglas Type
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 04 January 2019, pp. 119-130
- Print publication:
- March 2019
-
- Article
-
- You have access
- Export citation
EMBEDDING OF THE FREE ABELIAN TOPOLOGICAL GROUP
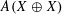 $A(X\oplus X)$ INTO
$A(X\oplus X)$ INTO 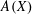 $A(X)$
$A(X)$
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 3 / 2019
- Published online by Cambridge University Press:
- 17 April 2019, pp. 708-718
- Print publication:
- 2019
-
- Article
- Export citation
POINT DISTRIBUTIONS IN TWO-POINT HOMOGENEOUS SPACES
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 3 / 2019
- Published online by Cambridge University Press:
- 26 March 2019, pp. 557-587
- Print publication:
- 2019
-
- Article
- Export citation
Delone dynamical systems and spectral convergence
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 6 / June 2020
- Published online by Cambridge University Press:
- 22 October 2018, pp. 1510-1544
- Print publication:
- June 2020
-
- Article
- Export citation
ON GENERALISED METRISABILITY AND CARDINAL INVARIANTS IN QUASITOPOLOGICAL GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 17 October 2018, pp. 302-310
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
Explicit asymptotic expansions for tame supercuspidal characters
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 11 / November 2018
- Published online by Cambridge University Press:
- 12 October 2018, pp. 2305-2378
- Print publication:
- November 2018
-
- Article
- Export citation
Spectral gap property and strong ergodicity for groups of affine transformations of solenoids
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 5 / May 2020
- Published online by Cambridge University Press:
- 11 October 2018, pp. 1180-1193
- Print publication:
- May 2020
-
- Article
- Export citation
Characters of inductive limits of finite alternating groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 4 / April 2020
- Published online by Cambridge University Press:
- 04 September 2018, pp. 1068-1082
- Print publication:
- April 2020
-
- Article
- Export citation
OPERATOR ALGEBRAIC APPROACH TO INVERSE AND STABILITY THEOREMS FOR AMENABLE GROUPS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 1 / 2019
- Published online by Cambridge University Press:
- 30 August 2018, pp. 98-118
- Print publication:
- 2019
-
- Article
- Export citation
LOCALLY COMPACT WREATH PRODUCTS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 15 August 2018, pp. 26-52
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
HARDY’S THEOREM FOR GABOR TRANSFORM
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 106 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 15 August 2018, pp. 143-159
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
Subgroup Correspondences
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 4 / November 2018
- Published online by Cambridge University Press:
- 14 August 2018, pp. 1127-1154
-
- Article
- Export citation
CHABAUTY LIMITS OF SIMPLE GROUPS ACTING ON TREES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 4 / July 2020
- Published online by Cambridge University Press:
- 06 August 2018, pp. 1093-1120
- Print publication:
- July 2020
-
- Article
- Export citation