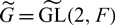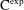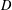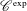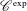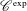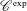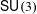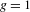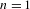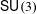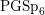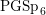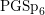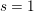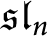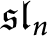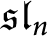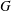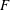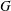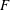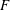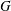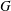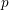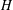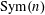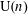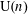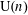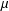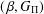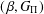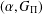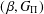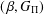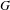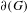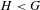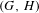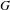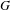Refine listing
Actions for selected content:
543 results in 22xxx
DUALIZING INVOLUTIONS ON THE METAPLECTIC GL(2) à la TUPAN
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 10 July 2020, pp. 426-437
- Print publication:
- May 2021
-
- Article
- Export citation
WAVE FRONT HOLONOMICITY OF
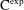 $\text{C}^{\text{exp}}$-CLASS DISTRIBUTIONS ON NON-ARCHIMEDEAN LOCAL FIELDS
$\text{C}^{\text{exp}}$-CLASS DISTRIBUTIONS ON NON-ARCHIMEDEAN LOCAL FIELDS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 30 June 2020, e35
-
- Article
-
- You have access
- Open access
- Export citation
DISTAL ACTIONS OF AUTOMORPHISMS OF NILPOTENT GROUPS G ON SUBG AND APPLICATIONS TO LATTICES IN LIE GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 23 June 2020, pp. 343-362
- Print publication:
- May 2021
-
- Article
- Export citation
The mapping class group action on
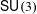 $\mathsf{SU}(3)$-character varieties
$\mathsf{SU}(3)$-character varieties
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 8 / August 2021
- Published online by Cambridge University Press:
- 15 June 2020, pp. 2382-2396
- Print publication:
- August 2021
-
- Article
-
- You have access
- Open access
- Export citation
A new characterization of the Haagerup property by actions on infinite measure spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 8 / August 2021
- Published online by Cambridge University Press:
- 02 June 2020, pp. 2349-2368
- Print publication:
- August 2021
-
- Article
- Export citation
An exceptional Siegel–Weil formula and poles of the Spin L-function of
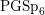 $\text{PGSp}_{6}$
$\text{PGSp}_{6}$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 6 / June 2020
- Published online by Cambridge University Press:
- 29 May 2020, pp. 1231-1261
- Print publication:
- June 2020
-
- Article
- Export citation
DECOMPOSITION THEOREMS FOR AUTOMORPHISM GROUPS OF TREES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 20 May 2020, pp. 104-112
- Print publication:
- February 2021
-
- Article
- Export citation
Categorification via blocks of modular representations for
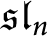 $\mathfrak {sl}_n$
$\mathfrak {sl}_n$
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 19 May 2020, pp. 1095-1123
- Print publication:
- August 2021
-
- Article
-
- You have access
- Open access
- Export citation
Données endoscopiques d’un groupe réductif connexe : applications d’une construction de Langlands
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 15 May 2020, pp. 1074-1094
- Print publication:
- August 2021
-
- Article
- Export citation
Finsler Warped Product Metrics with Relatively Isotropic Landsberg Curvature
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 12 May 2020, pp. 182-191
- Print publication:
- March 2021
-
- Article
- Export citation
Local Rankin–Selberg integrals for Speh representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 5 / May 2020
- Published online by Cambridge University Press:
- 13 April 2020, pp. 908-945
- Print publication:
- May 2020
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
QUOTIENTS OF ÉTALE GROUPOIDS AND THE ABELIANIZATIONS OF GROUPOID C*-ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 07 April 2020, pp. 56-75
- Print publication:
- August 2021
-
- Article
-
- You have access
- Open access
- Export citation
AN UNCERTAINTY PRINCIPLE FOR SOLUTIONS OF THE SCHRÖDINGER EQUATION ON
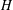 $H$-TYPE GROUPS
$H$-TYPE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 02 April 2020, pp. 1-16
- Print publication:
- August 2021
-
- Article
- Export citation
STABILITY, COHOMOLOGY VANISHING, AND NONAPPROXIMABLE GROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 30 March 2020, e18
-
- Article
-
- You have access
- Open access
- Export citation
ON
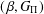 $(\,\unicode[STIX]{x1D6FD},G_{\unicode[STIX]{x1D6F1}})$-UNFAVOURABLE SPACES
$(\,\unicode[STIX]{x1D6FD},G_{\unicode[STIX]{x1D6F1}})$-UNFAVOURABLE SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 16 March 2020, pp. 439-450
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
FINITENESS OF TOPOLOGICAL ENTROPY FOR LOCALLY COMPACT ABELIAN GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 26 February 2020, pp. 81-105
- Print publication:
- January 2021
-
- Article
- Export citation
Furstenberg boundaries for pairs of groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 20 February 2020, pp. 1514-1529
- Print publication:
- May 2021
-
- Article
- Export citation
Amenable uniformly recurrent subgroups and lattice embeddings
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 07 February 2020, pp. 1464-1501
- Print publication:
- May 2021
-
- Article
- Export citation
Translates of Functions on the Heisenberg Group and the HRT Conjecture
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 03 February 2020, pp. 871-881
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
COMPARISON OF LOCAL RELATIVE CHARACTERS AND THE ICHINO–IKEDA CONJECTURE FOR UNITARY GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 22 January 2020, pp. 1803-1854
- Print publication:
- November 2021
-
- Article
- Export citation