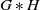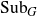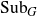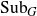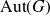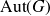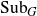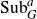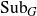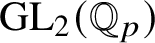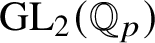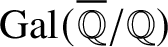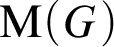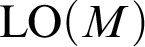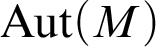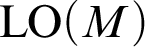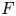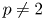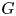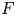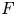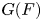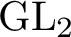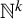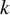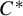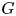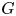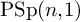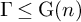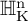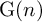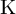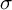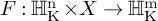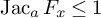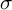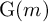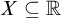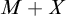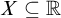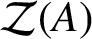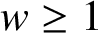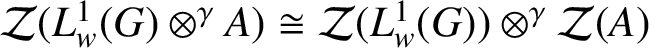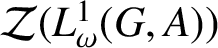Refine listing
Actions for selected content:
543 results in 22xxx
Weak amenability of free products of hyperbolic and amenable groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 06 January 2022, pp. 698-701
- Print publication:
- September 2022
-
- Article
- Export citation
Distal Actions of Automorphisms of Lie Groups G on SubG
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 2 / September 2022
- Published online by Cambridge University Press:
- 21 December 2021, pp. 457-478
- Print publication:
- September 2022
-
- Article
- Export citation
Finiteness properties of the category of mod p representations of
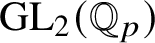 ${\textrm {GL}}_2 (\mathbb {Q}_{p})$
${\textrm {GL}}_2 (\mathbb {Q}_{p})$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 09 December 2021, e80
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Some Progress on the Unique Ergodicity Problem
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 27 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 28 February 2022, pp. 527-528
- Print publication:
- December 2021
-
- Article
-
- You have access
- Export citation
On the construction of tame supercuspidal representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 03 January 2022, pp. 2733-2746
- Print publication:
- December 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Fundamental local equivalences in quantum geometric Langlands
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 27 December 2021, pp. 2699-2732
- Print publication:
- December 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TRUNCATED AFFINE SPRINGER FIBERS AND ARTHUR’S WEIGHTED ORBITAL INTEGRALS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 10 November 2021, pp. 1757-1818
- Print publication:
- July 2023
-
- Article
- Export citation
Exponential mixing of frame flows for convex cocompact hyperbolic manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 08 November 2021, pp. 2585-2634
- Print publication:
- December 2021
-
- Article
- Export citation
Steenrod operators, the Coulomb branch and the Frobenius twist
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 04 November 2021, pp. 2494-2552
- Print publication:
- November 2021
-
- Article
- Export citation
The type semigroup, comparison, and almost finiteness for ample groupoids
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 27 October 2021, pp. 361-400
- Print publication:
- February 2023
-
- Article
- Export citation
Effective equidistribution for generalized higher-step nilflows
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 12 / December 2022
- Published online by Cambridge University Press:
- 25 October 2021, pp. 3656-3715
- Print publication:
- December 2022
-
- Article
- Export citation
Cocycles on groupoids arising from
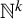 $\mathbb {N}^k$-actions
$\mathbb {N}^k$-actions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 11 / November 2022
- Published online by Cambridge University Press:
- 18 October 2021, pp. 3325-3356
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Boundary maps and maximal representations on infinite-dimensional Hermitian symmetric spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 18 October 2021, pp. 140-189
- Print publication:
- January 2023
-
- Article
- Export citation
TWISTS, CROSSED PRODUCTS AND INVERSE SEMIGROUP COHOMOLOGY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 114 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 08 October 2021, pp. 253-288
- Print publication:
- April 2023
-
- Article
- Export citation
On holomorphic reflexivity conditions for complex Lie groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 4 / November 2021
- Published online by Cambridge University Press:
- 30 September 2021, pp. 800-821
-
- Article
- Export citation
NATURAL MAPS FOR MEASURABLE COCYCLES OF COMPACT HYPERBOLIC MANIFOLDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 29 September 2021, pp. 421-448
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MEAGER-ADDITIVE SETS IN TOPOLOGICAL GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 27 September 2021, pp. 1046-1064
- Print publication:
- September 2022
-
- Article
- Export citation
An arithmetic property of intertwining operators for p-adic groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 17 September 2021, pp. 83-107
- Print publication:
- February 2023
-
- Article
- Export citation
CENTRE OF BANACH ALGEBRA VALUED BEURLING ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 13 September 2021, pp. 490-498
- Print publication:
- June 2022
-
- Article
- Export citation
Multiplicative constants and maximal measurable cocycles in bounded cohomology
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 11 / November 2022
- Published online by Cambridge University Press:
- 31 August 2021, pp. 3490-3525
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation