Refine listing
Actions for selected content:
543 results in 22xxx
The Finsler geometry of groups of isometries of Hilbert Space
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 42 / Issue 2 / April 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 196-222
- Print publication:
- April 1987
-
- Article
-
- You have access
- Export citation
Representations of minimally almost periodic groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 41 / Issue 3 / December 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 366-375
- Print publication:
- December 1986
-
- Article
-
- You have access
- Export citation
Primitive ideals with bounded approximate units in L1-algebras of exponential lie groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 41 / Issue 3 / December 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 411-420
- Print publication:
- December 1986
-
- Article
-
- You have access
- Export citation
Bilinear forms and 2-dimensional cohomology
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 41 / Issue 2 / October 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 165-179
- Print publication:
- October 1986
-
- Article
-
- You have access
- Export citation
Free products of topological groups with a closed subgroup amalgamated
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 40 / Issue 3 / June 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 414-420
- Print publication:
- June 1986
-
- Article
-
- You have access
- Export citation
The Akivis algebra of a homogeneous loop
- Part of
-
- Journal:
- Mathematika / Volume 33 / Issue 1 / June 1986
- Published online by Cambridge University Press:
- 26 February 2010, pp. 87-95
- Print publication:
- June 1986
-
- Article
- Export citation
The ~ -representations of symmetric homogeneous algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 40 / Issue 2 / April 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 267-275
- Print publication:
- April 1986
-
- Article
-
- You have access
- Export citation
Cocycles and representations of groups of CAR type
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 40 / Issue 1 / February 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 20-33
- Print publication:
- February 1986
-
- Article
-
- You have access
- Export citation
Special series of unitary representations of groups acting on homogeneous trees
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 40 / Issue 1 / February 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 83-88
- Print publication:
- February 1986
-
- Article
-
- You have access
- Export citation
Minimal F2-flows
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 39 / Issue 2 / October 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 187-193
- Print publication:
- October 1985
-
- Article
-
- You have access
- Export citation
Near-rings of mappings on finite topological groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 38 / Issue 1 / February 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 92-102
- Print publication:
- February 1985
-
- Article
-
- You have access
- Export citation
Some groups with T1 primitive ideal spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 38 / Issue 1 / February 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 55-64
- Print publication:
- February 1985
-
- Article
-
- You have access
- Export citation
A fundamental group topology
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 37 / Issue 3 / December 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 416-420
- Print publication:
- December 1984
-
- Article
-
- You have access
- Export citation
The von Neumann kernel of a locally compact group
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 36 / Issue 2 / April 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 279-286
- Print publication:
- April 1984
-
- Article
-
- You have access
- Export citation
Constructions of the maximal strongly character invariant segal algebras and their applications
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 35 / Issue 1 / August 1983
- Published online by Cambridge University Press:
- 09 April 2009, pp. 123-131
- Print publication:
- August 1983
-
- Article
-
- You have access
- Export citation
Certain semigroups embeddabable in topological groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 33 / Issue 1 / August 1982
- Published online by Cambridge University Press:
- 09 April 2009, pp. 30-39
- Print publication:
- August 1982
-
- Article
-
- You have access
- Export citation
Discrete groups whose multiplier representations are type I
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 31 / Issue 4 / December 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 486-495
- Print publication:
- December 1981
-
- Article
-
- You have access
- Export citation
Near-rings of continuous functions on disconnected groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 28 / Issue 4 / December 1979
- Published online by Cambridge University Press:
- 09 April 2009, pp. 433-451
- Print publication:
- December 1979
-
- Article
-
- You have access
- Export citation
A distal property of groups and the growth of connected locally compact groups
- Part of
-
- Journal:
- Mathematika / Volume 26 / Issue 1 / June 1979
- Published online by Cambridge University Press:
- 26 February 2010, pp. 94-98
- Print publication:
- June 1979
-
- Article
- Export citation
Semigroups over generalized trees
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 25 / Issue 2 / March 1978
- Published online by Cambridge University Press:
- 09 April 2009, pp. 177-188
- Print publication:
- March 1978
-
- Article
-
- You have access
- Export citation
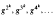 for some positive integer
for some positive integer 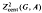 for certain 2-step nilpotent Lie groups
for certain 2-step nilpotent Lie groups 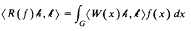
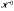 be the space of functions on the Poission boundary ω, of zero mean on ω. When
be the space of functions on the Poission boundary ω, of zero mean on ω. When 