Refine listing
Actions for selected content:
543 results in 22xxx
VARIETIES OF ABELIAN TOPOLOGICAL GROUPS AND SCATTERED SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 3 / December 2008
- Published online by Cambridge University Press:
- 01 December 2008, pp. 487-495
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
(GLn+1(F), GLn(F)) is a Gelfand pair for any local field F
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 6 / November 2008
- Published online by Cambridge University Press:
- 01 November 2008, pp. 1504-1524
- Print publication:
- November 2008
-
- Article
-
- You have access
- Export citation
OPERATOR KERNELS FOR IRREDUCIBLE REPRESENTATIONS OF EXPONENTIAL LIE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 2 / October 2008
- Published online by Cambridge University Press:
- 01 October 2008, pp. 301-316
- Print publication:
- October 2008
-
- Article
-
- You have access
- Export citation
Adiabatic limit of the eta invariant over cofinite quotients of PSL(2, ℝ)
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 6 / November 2008
- Published online by Cambridge University Press:
- 26 September 2008, pp. 1593-1616
- Print publication:
- November 2008
-
- Article
-
- You have access
- Export citation
On the classification of rank-two representations of quasiprojective fundamental groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 5 / September 2008
- Published online by Cambridge University Press:
- 01 September 2008, pp. 1271-1331
- Print publication:
- September 2008
-
- Article
-
- You have access
- Export citation
CONTINUITY OF MEASURABLE HOMOMORPHISMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 1 / August 2008
- Published online by Cambridge University Press:
- 01 August 2008, pp. 171-176
- Print publication:
- August 2008
-
- Article
-
- You have access
- Export citation
On the unramified spectrum of spherical varieties over p-adic fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 4 / July 2008
- Published online by Cambridge University Press:
- 01 July 2008, pp. 978-1016
- Print publication:
- July 2008
-
- Article
-
- You have access
- Export citation
CONTACT AND PANSU DIFFERENTIABLE MAPS ON CARNOT GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 3 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 495-507
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
Cohomology of topological groups with applications to the Weil group
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 3 / May 2008
- Published online by Cambridge University Press:
- 01 May 2008, pp. 633-656
- Print publication:
- May 2008
-
- Article
-
- You have access
- Export citation
On the restriction of representations of GL2(F) to a Borel subgroup
- Part of
-
- Journal:
- Compositio Mathematica / Volume 143 / Issue 6 / November 2007
- Published online by Cambridge University Press:
- 01 November 2007, pp. 1533-1544
- Print publication:
- November 2007
-
- Article
-
- You have access
- Export citation
An Open Mapping Theorem For Pro-Lie Groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 83 / Issue 1 / August 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 55-78
- Print publication:
- August 2007
-
- Article
-
- You have access
- Export citation
Local Homomorphisms of Topological Groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 83 / Issue 1 / August 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 135-148
- Print publication:
- August 2007
-
- Article
-
- You have access
- Export citation
The Gelfand transform of homogeneous distributions on Heisenberg type groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 81 / Issue 3 / December 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 297-319
- Print publication:
- December 2006
-
- Article
-
- You have access
- Export citation
Filter games and pathological subgroups of a countable product of lines
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 81 / Issue 3 / December 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 321-350
- Print publication:
- December 2006
-
- Article
-
- You have access
- Export citation
Kazhdan constants for compact groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 81 / Issue 1 / August 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 11-14
- Print publication:
- August 2006
-
- Article
-
- You have access
- Export citation
Estimates for kernels of intertwining operators on SL(n, R)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 81 / Issue 1 / August 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 105-120
- Print publication:
- August 2006
-
- Article
-
- You have access
- Export citation
Heat Kernels on homogeneous spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 78 / Issue 1 / February 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 109-147
- Print publication:
- February 2005
-
- Article
-
- You have access
- Export citation
The size of characters of exceptional lie groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 2 / October 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 233-248
- Print publication:
- October 2004
-
- Article
-
- You have access
- Export citation
Some regularity estimates for convolution semigroups on a group of polynomial growth
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 2 / October 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 249-268
- Print publication:
- October 2004
-
- Article
-
- You have access
- Export citation
An uncertainty principle like Hardy's theorem for nilpotent Lie groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 1 / August 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 47-54
- Print publication:
- August 2004
-
- Article
-
- You have access
- Export citation
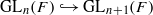 and the two-sided action of GL
and the two-sided action of GL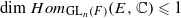 . For the proof in the archimedean case, we develop several tools to study invariant distributions on smooth manifolds.
. For the proof in the archimedean case, we develop several tools to study invariant distributions on smooth manifolds.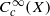 are in natural ‘almost bijection’ with a number of copies of
are in natural ‘almost bijection’ with a number of copies of 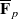 -vector spaces to
-vector spaces to 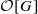 -modules of finite length and unitary
-modules of finite length and unitary 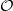 is the ring of integers of a complete discretely valued field
is the ring of integers of a complete discretely valued field 