Refine listing
Actions for selected content:
543 results in 22xxx
Characterization of lipschitz spaces on compact Lie groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 58 / Issue 2 / April 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 200-209
- Print publication:
- April 1995
-
- Article
-
- You have access
- Export citation
On the component group of the automorphism group of a Lie group
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 57 / Issue 3 / December 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 365-385
- Print publication:
- December 1994
-
- Article
-
- You have access
- Export citation
Subelliptic operators on Lie groups: regularity
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 57 / Issue 2 / October 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 179-229
- Print publication:
- October 1994
-
- Article
-
- You have access
- Export citation
Twisted crossed products by coactions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 56 / Issue 3 / June 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 320-344
- Print publication:
- June 1994
-
- Article
-
- You have access
- Export citation
Lp-functions satisfying the mean value property on homogeneous spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 56 / Issue 3 / June 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 384-390
- Print publication:
- June 1994
-
- Article
-
- You have access
- Export citation
Harmonic analysis for groups acting on triangle buildings
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 56 / Issue 3 / June 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 345-383
- Print publication:
- June 1994
-
- Article
-
- You have access
- Export citation
On the Fourier transform of a compact semisimple Lie group
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 56 / Issue 1 / February 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 64-116
- Print publication:
- February 1994
-
- Article
-
- You have access
- Export citation
Gevrey spaces and their intersections
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 54 / Issue 2 / April 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 263-286
- Print publication:
- April 1993
-
- Article
-
- You have access
- Export citation
Lacunary sets for groups and hypergroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 54 / Issue 1 / February 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 39-60
- Print publication:
- February 1993
-
- Article
-
- You have access
- Export citation
Duality for distributive bisemilattices
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 51 / Issue 2 / October 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 247-275
- Print publication:
- October 1991
-
- Article
-
- You have access
- Export citation
A note on Riesz sets and lacunary sets
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 48 / Issue 1 / February 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 57-65
- Print publication:
- February 1990
-
- Article
-
- You have access
- Export citation
The arithmetic structure of tetrahedral groups of hyperbolic isometries
- Part of
-
- Journal:
- Mathematika / Volume 36 / Issue 2 / December 1989
- Published online by Cambridge University Press:
- 26 February 2010, pp. 221-240
- Print publication:
- December 1989
-
- Article
- Export citation
Cartan subalgebras of regular extensions of von Neumann algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 45 / Issue 2 / October 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 249-274
- Print publication:
- October 1988
-
- Article
-
- You have access
- Export citation
On the characters of unitary representations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 45 / Issue 1 / August 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 62-65
- Print publication:
- August 1988
-
- Article
-
- You have access
- Export citation
A qualitative uncertainty principle for semisimple Lie groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 45 / Issue 1 / August 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 127-132
- Print publication:
- August 1988
-
- Article
-
- You have access
- Export citation
Hardy-Littlewood maximal functions on some solvable Lie groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 45 / Issue 1 / August 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 78-82
- Print publication:
- August 1988
-
- Article
-
- You have access
- Export citation
Certain Finitely Generated Compact Zero Dimensional Semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 44 / Issue 2 / April 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 265-270
- Print publication:
- April 1988
-
- Article
-
- You have access
- Export citation
LECs, Local Mixers, Topological Groups and Special Products
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 44 / Issue 2 / April 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 252-258
- Print publication:
- April 1988
-
- Article
-
- You have access
- Export citation
Motion Groups and Absolutely Convergent Fourier Transforms
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 43 / Issue 3 / December 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 385-397
- Print publication:
- December 1987
-
- Article
-
- You have access
- Export citation
Irreducibility of the analytic continuation of the principal series of a free group
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 43 / Issue 2 / October 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 199-210
- Print publication:
- October 1987
-
- Article
-
- You have access
- Export citation
 of
of 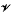 be its set of vertices. We study a commutative algebra
be its set of vertices. We study a commutative algebra 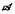 of ‘averaging’ operators acting on the space of complex valued functions on
of ‘averaging’ operators acting on the space of complex valued functions on  is valid. Examples are included.
is valid. Examples are included. of ℳ. we show that ℳ ⋊
of ℳ. we show that ℳ ⋊ 