Refine listing
Actions for selected content:
543 results in 22xxx
Banach-Dieudonné Theorem Revisited
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 75 / Issue 1 / August 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 69-83
- Print publication:
- August 2003
-
- Article
-
- You have access
- Export citation
Theta functions on Hermitian symmetric domains and fock representations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 2 / April 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 201-234
- Print publication:
- April 2003
-
- Article
-
- You have access
- Export citation
Paschke's conjecture for the endpoint anisotropic series representations of the free group
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 2 / April 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 173-184
- Print publication:
- April 2003
-
- Article
-
- You have access
- Export citation
Compact semilattices with open principal filters
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 3 / June 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 349-362
- Print publication:
- June 2002
-
- Article
-
- You have access
- Export citation
Some irreducible free group representations in which a linear combination of the generators has an eigenvalue
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 2 / April 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 257-286
- Print publication:
- April 2002
-
- Article
-
- You have access
- Export citation
On the Toeplitz algebras of right-angled and finite-type Artin groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 2 / April 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 223-246
- Print publication:
- April 2002
-
- Article
-
- You have access
- Export citation
Convexity of generalized numerical range associated with a compact Lie group
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 1 / February 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 57-66
- Print publication:
- February 2002
-
- Article
-
- You have access
- Export citation
Scale functions and tree ends
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 70 / Issue 2 / April 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 273-292
- Print publication:
- April 2001
-
- Article
-
- You have access
- Export citation
Pointwise estimates of the size of characters of compact Lie groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 69 / Issue 1 / August 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 61-84
- Print publication:
- August 2000
-
- Article
-
- You have access
- Export citation
Distance to the convex hull of an orbit under the action of a compact Lie group
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 66 / Issue 3 / June 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 331-357
- Print publication:
- June 1999
-
- Article
-
- You have access
- Export citation
Uncertainty principles like Hardy's theorem on some Lie groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 65 / Issue 3 / December 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 289-302
- Print publication:
- December 1998
-
- Article
-
- You have access
- Export citation
The Plancherel formula for the horocycle spaces and generalizations, II
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 65 / Issue 2 / October 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 194-211
- Print publication:
- October 1998
-
- Article
-
- You have access
- Export citation
Application of the Bruhat-Tits tree of SU3(h) to some Ã2 groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 3 / June 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 329-344
- Print publication:
- June 1998
-
- Article
-
- You have access
- Export citation
Cesàro kernels on classical groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 63 / Issue 3 / December 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 364-389
- Print publication:
- December 1997
-
- Article
-
- You have access
- Export citation
Second-order strongly elliptic operators on Lie groups with Hölder continuous coefficients
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 63 / Issue 3 / December 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 297-363
- Print publication:
- December 1997
-
- Article
-
- You have access
- Export citation
Equivariant holomorphic maps into the Siegel disc and the metaplectic representation
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 62 / Issue 2 / April 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 160-174
- Print publication:
- April 1997
-
- Article
-
- You have access
- Export citation
Derived intertwining norms for reducible spherical principal series
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 61 / Issue 2 / October 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 171-188
- Print publication:
- October 1996
-
- Article
-
- You have access
- Export citation
The Plancherel formula for the horocycle space and generalizations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 61 / Issue 1 / August 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 42-56
- Print publication:
- August 1996
-
- Article
-
- You have access
- Export citation
Weighted p-Sidon sets
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 61 / Issue 1 / August 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 73-95
- Print publication:
- August 1996
-
- Article
-
- You have access
- Export citation
On diameters of orbits of compact groups in unitary representations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 59 / Issue 3 / December 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 308-312
- Print publication:
- December 1995
-
- Article
-
- You have access
- Export citation
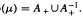 . Let λ be an endpoint of the spectrum of μ considered as a convolver on ℓ
. Let λ be an endpoint of the spectrum of μ considered as a convolver on ℓ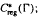 in particular, Paschke's conjecture holds for λ − μ.
in particular, Paschke's conjecture holds for λ − μ.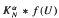 on the classical group
on the classical group 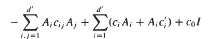 in divergence form corresponding to a quadratic form with complex coefficients, bounded Hölder continuous principal coefficients
in divergence form corresponding to a quadratic form with complex coefficients, bounded Hölder continuous principal coefficients 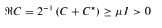 uniformly over
uniformly over 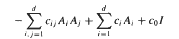 in non-divergence form for which the principal coefficients are at least once differentiable.
in non-divergence form for which the principal coefficients are at least once differentiable.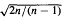 if
if 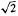 if
if 