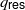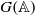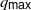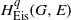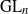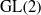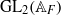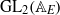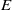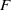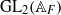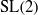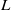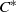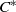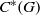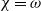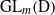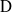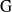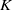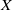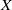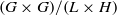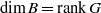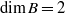Refine listing
Actions for selected content:
543 results in 22xxx
On the arithmetic fundamental lemma in the minuscule case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 10 / October 2013
- Published online by Cambridge University Press:
- 04 July 2013, pp. 1631-1666
- Print publication:
- October 2013
-
- Article
- Export citation
TOWARDS DIFFERENTIAL CALCULUS IN STRATIFIED GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 95 / Issue 1 / August 2013
- Published online by Cambridge University Press:
- 17 June 2013, pp. 76-128
- Print publication:
- August 2013
-
- Article
-
- You have access
- Export citation
SUBGROUPS OF FRACTIONAL DIMENSION IN NILPOTENT OR SOLVABLE LIE GROUPS
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 2 / July 2013
- Published online by Cambridge University Press:
- 23 May 2013, pp. 497-511
- Print publication:
- July 2013
-
- Article
- Export citation
Residues of Eisenstein series and the automorphic cohomology of reductive groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 7 / July 2013
- Published online by Cambridge University Press:
- 07 May 2013, pp. 1061-1090
- Print publication:
- July 2013
-
- Article
- Export citation
A local-global question in automorphic forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 6 / June 2013
- Published online by Cambridge University Press:
- 26 April 2013, pp. 959-995
- Print publication:
- June 2013
-
- Article
- Export citation
GROUPOID
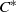 ${C}^{\ast } $-ALGEBRAS WITH HAUSDORFF SPECTRUM
${C}^{\ast } $-ALGEBRAS WITH HAUSDORFF SPECTRUM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 08 March 2013, pp. 232-242
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
A NOTE ON FREE ACTIONS OF GROUPS ON PRODUCTS OF SPHERES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 08 March 2013, pp. 340-344
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
Cusp eigenforms and the hall algebra of an elliptic curve
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 6 / June 2013
- Published online by Cambridge University Press:
- 04 March 2013, pp. 914-958
- Print publication:
- June 2013
-
- Article
- Export citation
On the Iwasawa theory of the Lubin–Tate moduli space
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 5 / May 2013
- Published online by Cambridge University Press:
- 26 February 2013, pp. 793-839
- Print publication:
- May 2013
-
- Article
- Export citation
THE MULTIPLIER ALGEBRA AND BSE PROPERTY OF THE DIRECT SUM OF BANACH ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 07 February 2013, pp. 250-258
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
Représentations banales de
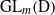 ${\rm GL}_{m}({\rm D})$
${\rm GL}_{m}({\rm D})$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 4 / April 2013
- Published online by Cambridge University Press:
- 02 January 2013, pp. 679-704
- Print publication:
- April 2013
-
- Article
- Export citation
Representations of metaplectic groups I: epsilon dichotomy and local Langlands correspondence
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 6 / November 2012
- Published online by Cambridge University Press:
- 31 October 2012, pp. 1655-1694
- Print publication:
- November 2012
-
- Article
-
- You have access
- Export citation
NOTES ON
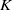 $K$-TOPOLOGICAL GROUPS AND HOMEOMORPHISMS OF TOPOLOGICAL GROUPS
$K$-TOPOLOGICAL GROUPS AND HOMEOMORPHISMS OF TOPOLOGICAL GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 30 August 2012, pp. 493-502
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
VISIBLE ACTIONS ON FLAG VARIETIES OF TYPE B AND A GENERALISATION OF THE CARTAN DECOMPOSITION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 1 / August 2013
- Published online by Cambridge University Press:
- 20 August 2012, pp. 81-97
- Print publication:
- August 2013
-
- Article
-
- You have access
- Export citation
Boundary behaviour of special cohomology classes arising from the Weil representation
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 12 / Issue 3 / July 2013
- Published online by Cambridge University Press:
- 03 July 2012, pp. 571-634
- Print publication:
- July 2013
-
- Article
- Export citation
Laguerre semigroup and Dunkl operators
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 4 / July 2012
- Published online by Cambridge University Press:
- 18 May 2012, pp. 1265-1336
- Print publication:
- July 2012
-
- Article
-
- You have access
- Export citation
Duality for nonlinear simply laced groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 3 / May 2012
- Published online by Cambridge University Press:
- 19 March 2012, pp. 931-965
- Print publication:
- May 2012
-
- Article
-
- You have access
- Export citation
Quantifying residual finiteness of arithmetic groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 3 / May 2012
- Published online by Cambridge University Press:
- 19 March 2012, pp. 907-920
- Print publication:
- May 2012
-
- Article
-
- You have access
- Export citation
Théorème de Paley—Wiener pour les fonctions de Whittaker sur un groupe réductif p-adique
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 11 / Issue 3 / July 2012
- Published online by Cambridge University Press:
- 06 January 2012, pp. 501-568
- Print publication:
- July 2012
-
- Article
- Export citation
Generalized affine Springer fibres
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 11 / Issue 3 / July 2012
- Published online by Cambridge University Press:
- 03 January 2012, pp. 569-609
- Print publication:
- July 2012
-
- Article
- Export citation