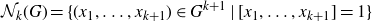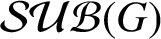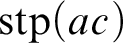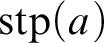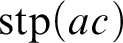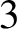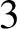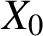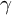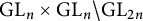Refine listing
Actions for selected content:
543 results in 22xxx
Harmonic models and Bernoullicity
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 19 August 2021, pp. 2160-2198
- Print publication:
- October 2021
-
- Article
- Export citation
Annihilator varieties of distinguished modules of reductive Lie algebras
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 26 July 2021, e52
-
- Article
-
- You have access
- Open access
- Export citation
A construction of complex analytic elliptic cohomology from double free loop spaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 8 / August 2021
- Published online by Cambridge University Press:
- 26 July 2021, pp. 1853-1897
- Print publication:
- August 2021
-
- Article
- Export citation
Compact groups with a set of positive Haar measure satisfying a nilpotent law
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 2 / September 2022
- Published online by Cambridge University Press:
- 19 July 2021, pp. 329-332
- Print publication:
- September 2022
-
- Article
- Export citation
Diagrams in the mod p cohomology of Shimura curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 8 / August 2021
- Published online by Cambridge University Press:
- 07 July 2021, pp. 1653-1723
- Print publication:
- August 2021
-
- Article
- Export citation
Chief factors in Polish groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 2 / September 2022
- Published online by Cambridge University Press:
- 30 June 2021, pp. 239-296
- Print publication:
- September 2022
-
- Article
- Export citation
Unique ergodicity of the automorphism group of the semigeneric directed graph
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 8 / August 2022
- Published online by Cambridge University Press:
- 28 June 2021, pp. 2561-2574
- Print publication:
- August 2022
-
- Article
- Export citation
Corrigendum: On the cuspidal cohomology of S-arithmetic subgroups of reductive groups over number fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 6 / June 2021
- Published online by Cambridge University Press:
- 26 May 2021, pp. 1207-1210
- Print publication:
- June 2021
-
- Article
-
- You have access
- HTML
- Export citation
ON THE CONNECTEDNESS OF THE CHABAUTY SPACE OF A LOCALLY COMPACT PRONILPOTENT GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 17 May 2021, pp. 161-170
- Print publication:
- February 2022
-
- Article
- Export citation
Oscillating multipliers on symmetric and locally symmetric spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 14 May 2021, pp. 887-905
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE RELATIVIZED LASCAR GROUPS, TYPE-AMALGAMATION, AND ALGEBRAICITY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 06 May 2021, pp. 531-557
- Print publication:
- June 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Geodesic planes in geometrically finite acylindrical
 $3$-manifolds
$3$-manifolds
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 04 May 2021, pp. 514-553
- Print publication:
- February 2022
-
- Article
- Export citation
THE SMOOTHNESS OF ORBITAL MEASURES ON NONCOMPACT SYMMETRIC SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 26 April 2021, pp. 188-207
- Print publication:
- October 2022
-
- Article
- Export citation
Arithmeticity of hyperbolic
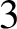 $3$-manifolds containing infinitely many totally geodesic surfaces
$3$-manifolds containing infinitely many totally geodesic surfaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 22 April 2021, pp. 1188-1219
- Print publication:
- March 2022
-
- Article
- Export citation
INVARIANT SETS AND NORMAL SUBGROUPOIDS OF UNIVERSAL ÉTALE GROUPOIDS INDUCED BY CONGRUENCES OF INVERSE SEMIGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 13 April 2021, pp. 99-118
- Print publication:
- August 2022
-
- Article
-
- You have access
- Open access
- Export citation
ON GRAEV’S THEOREM FOR FREE PRODUCTS OF HAUSDORFF TOPOLOGICAL GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 29 March 2021, pp. 475-483
- Print publication:
- December 2021
-
- Article
- Export citation
ON FORMAL DEGREES OF UNIPOTENT REPRESENTATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 19 March 2021, pp. 1947-1999
- Print publication:
- November 2022
-
- Article
- Export citation
R-GROUP AND WHITTAKER SPACE OF SOME GENUINE REPRESENTATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 08 March 2021, pp. 213-273
- Print publication:
- January 2023
-
- Article
- Export citation
Orbital integrals on
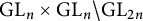 $\text{GL}_n \times \text{GL}_n \backslash \text{GL}_{2n}$
$\text{GL}_n \times \text{GL}_n \backslash \text{GL}_{2n}$
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 26 February 2021, pp. 858-886
- Print publication:
- June 2022
-
- Article
- Export citation
Le transfert singulier pour la formule des traces de Jacquet–Rallis
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 16 March 2021, pp. 303-434
- Print publication:
- February 2021
-
- Article
- Export citation