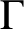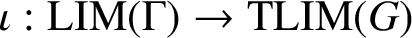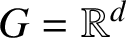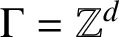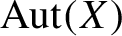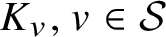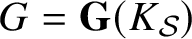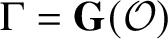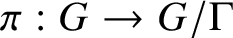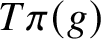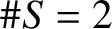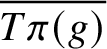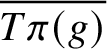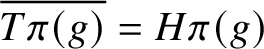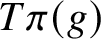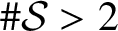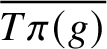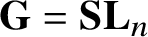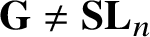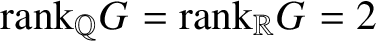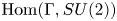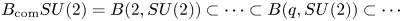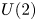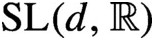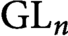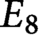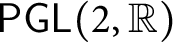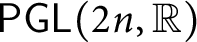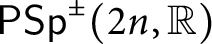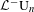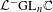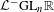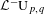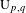Refine listing
Actions for selected content:
543 results in 22xxx
A BIJECTION OF INVARIANT MEANS ON AN AMENABLE GROUP WITH THOSE ON A LATTICE SUBGROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 18 January 2021, pp. 302-307
- Print publication:
- October 2021
-
- Article
- Export citation
ON A CERTAIN LOCAL IDENTITY FOR LAPID–MAO’S CONJECTURE AND FORMAL DEGREE CONJECTURE : EVEN UNITARY GROUP CASE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 08 January 2021, pp. 1107-1161
- Print publication:
- July 2022
-
- Article
- Export citation
Minimal flows with arbitrary centralizer
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 29 December 2020, pp. 310-320
- Print publication:
- January 2022
-
- Article
- Export citation
On Polish groups admitting non-essentially countable actions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 29 December 2020, pp. 180-194
- Print publication:
- January 2022
-
- Article
-
- You have access
- Open access
- Export citation
Compact groups in which all elements have countable right Engel sinks
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 13 November 2020, pp. 1790-1814
- Print publication:
- December 2021
-
- Article
- Export citation
Closures of locally divergent orbits of maximal tori and values of homogeneous forms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 05 November 2020, pp. 3142-3177
- Print publication:
- October 2021
-
- Article
- Export citation
Divergent trajectories in arithmetic homogeneous spaces of rational rank two
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 05 November 2020, pp. 3116-3141
- Print publication:
- October 2021
-
- Article
-
- You have access
- Open access
- Export citation
Vanishing of cohomology and parameter rigidity of actions of solvable Lie groups, II
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 03 November 2020, pp. 3023-3059
- Print publication:
- October 2021
-
- Article
-
- You have access
- Open access
- Export citation
Sup-norms of eigenfunctions in the level aspect for compact arithmetic surfaces, II: newforms and subconvexity
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 11 / November 2020
- Published online by Cambridge University Press:
- 15 December 2020, pp. 2368-2398
- Print publication:
- November 2020
-
- Article
- Export citation
Branching laws for classical groups: the non-tempered case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 11 / November 2020
- Published online by Cambridge University Press:
- 17 December 2020, pp. 2298-2367
- Print publication:
- November 2020
-
- Article
- Export citation
Autocorrelation functions for quantum particles in supersymmetric Pöschl-Teller potentials
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 28 October 2020, pp. 840-852
- Print publication:
- December 2021
-
- Article
- Export citation
Cardinal invariants of Haar null and Haar meager sets
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 27 October 2020, pp. 1568-1594
- Print publication:
- October 2021
-
- Article
-
- You have access
- Open access
- Export citation
Limits of geodesic push-forwards of horocycle invariant measures
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 9 / September 2021
- Published online by Cambridge University Press:
- 23 October 2020, pp. 2782-2804
- Print publication:
- September 2021
-
- Article
- Export citation
Spread out random walks on homogeneous spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 06 October 2020, pp. 3439-3473
- Print publication:
- November 2021
-
- Article
- Export citation
Nilpotent n-tuples in SU(2)
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 4 / November 2020
- Published online by Cambridge University Press:
- 30 September 2020, pp. 1005-1030
-
- Article
- Export citation
Arithmeticity of discrete subgroups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 9 / September 2021
- Published online by Cambridge University Press:
- 28 September 2020, pp. 2561-2590
- Print publication:
- September 2021
-
- Article
- Export citation
Fourier coefficients of minimal and next-to-minimal automorphic representations of simply-laced groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 21 September 2020, pp. 122-169
- Print publication:
- February 2022
-
- Article
-
- You have access
- Open access
- Export citation
Rigidity of diagonally embedded triangle groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 20 August 2020, pp. 560-579
- Print publication:
- September 2021
-
- Article
- Export citation
PROJECTIVE LOOPS GENERATE RATIONAL LOOP GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 17 August 2020, pp. 459-485
- Print publication:
- March 2022
-
- Article
- Export citation
Étale groupoid algebras with coefficients in a sheaf and skew inverse semigroup rings
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 07 August 2020, pp. 1592-1626
- Print publication:
- December 2021
-
- Article
- Export citation