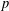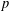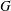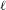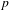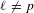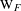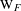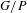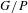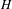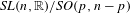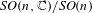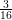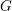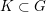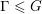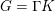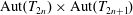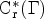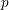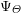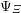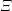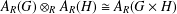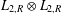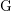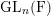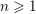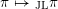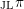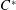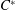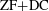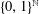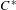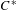Refine listing
Actions for selected content:
543 results in 22xxx
Matching of orbital integrals (transfer) and Roche Hecke algebra isomorphisms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 3 / March 2020
- Published online by Cambridge University Press:
- 21 January 2020, pp. 533-603
- Print publication:
- March 2020
-
- Article
- Export citation
ON THE EXISTENCE OF ADMISSIBLE SUPERSINGULAR REPRESENTATIONS OF
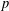 $p$-ADIC REDUCTIVE GROUPS
$p$-ADIC REDUCTIVE GROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 13 January 2020, e2
-
- Article
-
- You have access
- Open access
- Export citation
Separable Quotients of Free Topological Groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 29 November 2019, pp. 610-623
- Print publication:
- September 2020
-
- Article
-
- You have access
- Export citation
Super-rigidity and non-linearity for lattices in products
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 26 November 2019, pp. 158-178
- Print publication:
- January 2020
-
- Article
- Export citation
THE
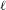 $\ell$-MODULAR LOCAL LANGLANDS CORRESPONDENCE AND LOCAL CONSTANTS
$\ell$-MODULAR LOCAL LANGLANDS CORRESPONDENCE AND LOCAL CONSTANTS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 5 / September 2021
- Published online by Cambridge University Press:
- 08 November 2019, pp. 1585-1635
- Print publication:
- September 2021
-
- Article
- Export citation
GEOMETRY OF KOTTWITZ–VIEHMANN VARIETIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 08 November 2019, pp. 1-65
- Print publication:
- January 2022
-
- Article
- Export citation
BOREL DENSITY FOR APPROXIMATE LATTICES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 05 November 2019, e40
-
- Article
-
- You have access
- Open access
- Export citation
PARABOLIC COMPACTIFICATION OF HOMOGENEOUS SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 4 / July 2021
- Published online by Cambridge University Press:
- 30 October 2019, pp. 1371-1408
- Print publication:
- July 2021
-
- Article
- Export citation
On Selberg’s eigenvalue conjecture for moduli spaces of abelian differentials
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 12 / December 2019
- Published online by Cambridge University Press:
- 30 October 2019, pp. 2354-2398
- Print publication:
- December 2019
-
- Article
- Export citation
Bounding the covolume of lattices in products
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 12 / December 2019
- Published online by Cambridge University Press:
- 11 October 2019, pp. 2296-2333
- Print publication:
- December 2019
-
- Article
- Export citation
New Simple Lattices in Products of Trees and their Projections
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 07 October 2019, pp. 1624-1690
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
POLYNOMIAL COHOMOLOGY AND POLYNOMIAL MAPS ON NILPOTENT GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 02 October 2019, pp. 706-736
- Print publication:
- September 2020
-
- Article
-
- You have access
- Export citation
Escaping a Neighborhood Along a Prescribed Sequence in Lie Groups and Banach Algebras
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 02 October 2019, pp. 484-505
- Print publication:
- September 2020
-
- Article
-
- You have access
- Export citation
On pathological properties of fixed point algebras in Kirchberg algebras
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 20 September 2019, pp. 3087-3096
- Print publication:
- December 2020
-
- Article
- Export citation
Local Langlands correspondence and ramification for Carayol representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 10 / October 2019
- Published online by Cambridge University Press:
- 06 September 2019, pp. 1959-2038
- Print publication:
- October 2019
-
- Article
-
- You have access
- HTML
- Export citation
TENSOR PRODUCTS OF STEINBERG ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 04 September 2019, pp. 111-126
- Print publication:
- August 2021
-
- Article
- Export citation
Towards an explicit local Jacquet–Langlands correspondence beyond the cuspidal case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 10 / October 2019
- Published online by Cambridge University Press:
- 27 August 2019, pp. 1853-1887
- Print publication:
- October 2019
-
- Article
- Export citation
GCR and CCR Steinberg Algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 23 August 2019, pp. 1581-1606
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
CONTINUITY OF UNIVERSALLY MEASURABLE HOMOMORPHISMS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 7 / 2019
- Published online by Cambridge University Press:
- 13 August 2019, e5
-
- Article
-
- You have access
- Open access
- Export citation
On graph products of multipliers and the Haagerup property for
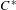 $C^{\ast }$-dynamical systems
$C^{\ast }$-dynamical systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 07 August 2019, pp. 3188-3216
- Print publication:
- December 2020
-
- Article
- Export citation