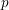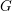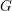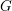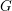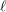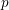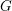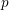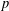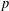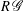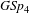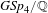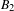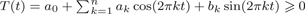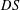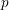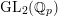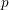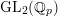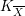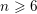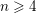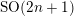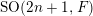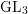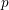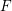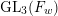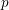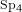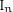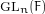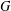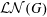Refine listing
Actions for selected content:
543 results in 22xxx
Nearby cycles of Whittaker sheaves on Drinfeld’s compactification
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 8 / August 2018
- Published online by Cambridge University Press:
- 18 July 2018, pp. 1775-1800
- Print publication:
- August 2018
-
- Article
- Export citation
INTERTWINING SEMISIMPLE CHARACTERS FOR
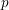 $p$-ADIC CLASSICAL GROUPS
$p$-ADIC CLASSICAL GROUPS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 238 / June 2020
- Published online by Cambridge University Press:
- 16 July 2018, pp. 137-205
- Print publication:
- June 2020
-
- Article
-
- You have access
- HTML
- Export citation
Sur les
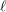 $\ell$ -blocs de niveau zéro des groupes
$\ell$ -blocs de niveau zéro des groupes 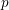 $p$ -adiques
$p$ -adiques
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 7 / July 2018
- Published online by Cambridge University Press:
- 24 May 2018, pp. 1473-1507
- Print publication:
- July 2018
-
- Article
- Export citation
Arithmetic intersection on GSpin Rapoport–Zink spaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 7 / July 2018
- Published online by Cambridge University Press:
- 16 May 2018, pp. 1407-1440
- Print publication:
- July 2018
-
- Article
- Export citation
On Følner sets in topological groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 7 / July 2018
- Published online by Cambridge University Press:
- 16 May 2018, pp. 1333-1361
- Print publication:
- July 2018
-
- Article
- Export citation
COCENTERS OF
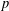 $p$ -ADIC GROUPS, I: NEWTON DECOMPOSITION
$p$ -ADIC GROUPS, I: NEWTON DECOMPOSITION
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 6 / 2018
- Published online by Cambridge University Press:
- 28 March 2018, e2
-
- Article
-
- You have access
- Open access
- Export citation
CHAIN CONDITIONS ON ÉTALE GROUPOID ALGEBRAS WITH APPLICATIONS TO LEAVITT PATH ALGEBRAS AND INVERSE SEMIGROUP ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 28 March 2018, pp. 403-411
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
AN EQUIDISTRIBUTION THEOREM FOR HOLOMORPHIC SIEGEL MODULAR FORMS FOR
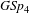 $\mathit{GSp}_{4}$ AND ITS APPLICATIONS
$\mathit{GSp}_{4}$ AND ITS APPLICATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 22 February 2018, pp. 351-419
- Print publication:
- March 2020
-
- Article
- Export citation
The Point Value Maximization Problem for Positive Definite Functions Supported in a Given Subset of a Locally Compact Group
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 24 January 2018, pp. 179-200
-
- Article
- Export citation
WEAK ADMISSIBILITY, PRIMITIVITY, O-MINIMALITY, AND DIOPHANTINE APPROXIMATION
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 2 / 2018
- Published online by Cambridge University Press:
- 17 April 2018, pp. 475-496
- Print publication:
- 2018
-
- Article
- Export citation
DENSITY, SMITAL PROPERTY AND QUASICONTINUITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 04 December 2017, pp. 246-252
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
Patching and the
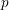 $p$ -adic Langlands program for
$p$ -adic Langlands program for 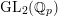 $\operatorname{GL}_{2}(\mathbb{Q}_{p})$
$\operatorname{GL}_{2}(\mathbb{Q}_{p})$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 3 / March 2018
- Published online by Cambridge University Press:
- 01 December 2017, pp. 503-548
- Print publication:
- March 2018
-
- Article
- Export citation
The Kodaira dimension of complex hyperbolic manifolds with cusps
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 3 / March 2018
- Published online by Cambridge University Press:
- 28 November 2017, pp. 549-564
- Print publication:
- March 2018
-
- Article
- Export citation
REPRÉSENTATIONS DE RÉDUCTION UNIPOTENTE POUR
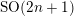 $\operatorname{SO}(2n+1)$, II : ENDOSCOPIE
$\operatorname{SO}(2n+1)$, II : ENDOSCOPIE
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 233 / March 2019
- Published online by Cambridge University Press:
- 21 September 2017, pp. 87-154
- Print publication:
- March 2019
-
- Article
-
- You have access
- HTML
- Export citation
On mod
 $p$ local-global compatibility for
$p$ local-global compatibility for 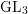 $\text{GL}_{3}$ in the ordinary case
$\text{GL}_{3}$ in the ordinary case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 11 / November 2017
- Published online by Cambridge University Press:
- 25 August 2017, pp. 2215-2286
- Print publication:
- November 2017
-
- Article
- Export citation
A VARIANT OF HARISH-CHANDRA FUNCTORS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 5 / September 2019
- Published online by Cambridge University Press:
- 14 August 2017, pp. 993-1049
- Print publication:
- September 2019
-
- Article
- Export citation
WHITTAKER FUNCTIONS AND DEMAZURE CHARACTERS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 4 / July 2019
- Published online by Cambridge University Press:
- 22 June 2017, pp. 759-781
- Print publication:
- July 2019
-
- Article
- Export citation
LOCALLY NORMAL SUBGROUPS OF TOTALLY DISCONNECTED GROUPS. PART II: COMPACTLY GENERATED SIMPLE GROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 22 May 2017, e12
-
- Article
-
- You have access
- Open access
- Export citation
CANNON–THURSTON MAPS FOR KLEINIAN GROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 5 / 2017
- Published online by Cambridge University Press:
- 22 May 2017, e1
-
- Article
-
- You have access
- Open access
- Export citation
LOCALLY NORMAL SUBGROUPS OF TOTALLY DISCONNECTED GROUPS. PART I: GENERAL THEORY
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 22 May 2017, e11
-
- Article
-
- You have access
- Open access
- Export citation