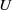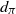Refine search
Actions for selected content:
52379 results in Statistics and Probability
A transport process on graphs and its limiting distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 10 October 2022, pp. 341-357
- Print publication:
- March 2023
-
- Article
- Export citation
Eliminating proxy errors from capital estimates by targeted exact computation
-
- Journal:
- Annals of Actuarial Science / Volume 17 / Issue 2 / July 2023
- Published online by Cambridge University Press:
- 07 October 2022, pp. 219-242
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Epidemiology and bacterial characteristics of invasive group B streptococcus disease: a population-based study in Japan in 2010–2020
-
- Journal:
- Epidemiology & Infection / Volume 150 / 2022
- Published online by Cambridge University Press:
- 07 October 2022, e184
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Anomalous recurrence of Markov chains on negatively curved manifolds
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 06 October 2022, pp. 204-222
- Print publication:
- March 2023
-
- Article
- Export citation
Northern Ireland farm-level management factors for recurrent bovine tuberculosis herd breakdowns
-
- Journal:
- Epidemiology & Infection / Volume 150 / 2022
- Published online by Cambridge University Press:
- 05 October 2022, e176
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Polynomials over structured grids
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 04 October 2022, pp. 284-298
-
- Article
- Export citation
Household transmission of the Delta COVID-19 variant in Queensland, Australia: a case series
-
- Journal:
- Epidemiology & Infection / Volume 150 / 2022
- Published online by Cambridge University Press:
- 04 October 2022, e173
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Lesson (un)replicated: Predicting levels of political violence in Afghan administrative units per month using ARFIMA and ICEWS data
-
- Journal:
- Data & Policy / Volume 4 / 2022
- Published online by Cambridge University Press:
- 04 October 2022, e32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sparse recovery properties of discrete random matrices
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 04 October 2022, pp. 316-325
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stationary analysis of an (R, Q) inventory model with normal and emergency orders
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 04 October 2022, pp. 106-126
- Print publication:
- March 2023
-
- Article
- Export citation
Improved bound for improper colourings of graphs with no odd clique minor
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 30 September 2022, pp. 326-333
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Multivariate Poisson and Poisson process approximations with applications to Bernoulli sums and
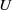 $U$-statistics
$U$-statistics
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 30 September 2022, pp. 223-240
- Print publication:
- March 2023
-
- Article
-
- You have access
- HTML
- Export citation
A stochastic model for capital requirement assessment for mortality and longevity risk, focusing on idiosyncratic and trend components
-
- Journal:
- Annals of Actuarial Science / Volume 16 / Issue 3 / November 2022
- Published online by Cambridge University Press:
- 30 September 2022, pp. 527-546
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Index
-
- Book:
- Principles of Data Assimilation
- Published online:
- 22 September 2022
- Print publication:
- 29 September 2022, pp 384-398
-
- Chapter
- Export citation
4 - Tangent Linear and Adjoint Models
- from Part II - Practical Tools
-
- Book:
- Principles of Data Assimilation
- Published online:
- 22 September 2022
- Print publication:
- 29 September 2022, pp 83-110
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Principles of Data Assimilation
- Published online:
- 22 September 2022
- Print publication:
- 29 September 2022, pp i-iv
-
- Chapter
- Export citation
Appendix A - Linear Algebra and Functional Analysis
- from Part V - Appendices
-
- Book:
- Principles of Data Assimilation
- Published online:
- 22 September 2022
- Print publication:
- 29 September 2022, pp 333-346
-
- Chapter
- Export citation
Part III - Methods and Issues
-
- Book:
- Principles of Data Assimilation
- Published online:
- 22 September 2022
- Print publication:
- 29 September 2022, pp 161-162
-
- Chapter
- Export citation
11 - Sensitivity Analysis and Adaptive Observation
- from Part IV - Applications
-
- Book:
- Principles of Data Assimilation
- Published online:
- 22 September 2022
- Print publication:
- 29 September 2022, pp 265-304
-
- Chapter
- Export citation
Appendix B - Discretization of Partial Differential Equations
- from Part V - Appendices
-
- Book:
- Principles of Data Assimilation
- Published online:
- 22 September 2022
- Print publication:
- 29 September 2022, pp 347-352
-
- Chapter
- Export citation