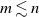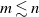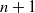Refine search
Actions for selected content:
52651 results in Statistics and Probability
HIV care continuum outcomes among recently diagnosed people with HIV (PWH) in Washington, DC
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 30 January 2023, e45
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Multiple-drawing dynamic Friedman urns with opposite-reinforcement
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 26 January 2023, pp. 115-129
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Invasive pneumococcal surveillance to assess the potential benefits of extended spectrum conjugate vaccines (PCV15/PCV20) in older adults
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 26 January 2023, e27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mean flow reconstruction of unsteady flows using physics-informed neural networks
-
- Journal:
- Data-Centric Engineering / Volume 4 / 2023
- Published online by Cambridge University Press:
- 25 January 2023, e4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A simplest mathematics of turn-taking: Conversational deep structure, emergence, and permeation
-
- Journal:
- Network Science / Volume 11 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 25 January 2023, pp. 224-248
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Effects of haptic imagery on purchase intention
-
- Journal:
- Experimental Results / Volume 4 / 2023
- Published online by Cambridge University Press:
- 25 January 2023, e4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Preferential attachment hypergraph with high modularity
-
- Journal:
- Network Science / Volume 10 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 23 January 2023, pp. 400-429
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NWS volume 10 issue 4 Cover and Front matter
-
- Journal:
- Network Science / Volume 10 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 23 January 2023, pp. f1-f3
-
- Article
-
- You have access
- Export citation
Expanding the boundaries of interdisciplinary field: Contribution of Network Science journal to the development of network science
-
- Journal:
- Network Science / Volume 11 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 20 January 2023, pp. 65-97
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimal control of supervisors balancing individual and joint responsibilities
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 20 January 2023, pp. 130-149
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quality issues in co-authorship data of a national scientific community
-
- Journal:
- Network Science / Volume 11 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 20 January 2023, pp. 98-112
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sturm–Liouville theory and decay parameter for quadratic markov branching processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 19 January 2023, pp. 737-764
- Print publication:
- September 2023
-
- Article
- Export citation
Trichinella infection in Serbia from 2011 to 2020: a success story in the field of One Health
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 19 January 2023, e20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A large A(H3N2) influenza outbreak with a high attack rate in a drug user community in Italy, April 2022
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 19 January 2023, e36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PES volume 37 issue 1 Cover
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 37 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 18 January 2023, p. f1
-
- Article
-
- You have access
- Export citation
Relationships between cumulative entropy/extropy, Gini mean difference and probability weighted moments
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 18 January 2023, pp. 28-38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Critical branching as a pure death process coming down from infinity
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 18 January 2023, pp. 607-628
- Print publication:
- June 2023
-
- Article
- Export citation
Use of portable air purifiers to reduce aerosols in hospital settings and cut down the clinical backlog
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 18 January 2023, e21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Parking functions: interdisciplinary connections
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 17 January 2023, pp. 768-792
- Print publication:
- September 2023
-
- Article
- Export citation
RELEVANT MOMENT SELECTION UNDER MIXED IDENTIFICATION STRENGTH
-
- Journal:
- Econometric Theory / Volume 40 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 16 January 2023, pp. 1003-1064
-
- Article
-
- You have access
- Open access
- Export citation