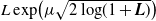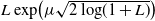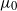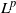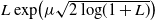Refine search
Actions for selected content:
52379 results in Statistics and Probability
SEQUENTIALLY ESTIMATING THE STRUCTURAL EQUATION BY POWER TRANSFORMATION
-
- Journal:
- Econometric Theory / Volume 40 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 19 September 2022, pp. 98-161
-
- Article
- Export citation
Distribution-based packet forwarding distance dissimilarity learning for topology characterizing in geographic routing
-
- Journal:
- Experimental Results / Volume 3 / 2022
- Published online by Cambridge University Press:
- 19 September 2022, e19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
From reflected Lévy processes to stochastically monotone Markov processes via generalized inverses and supermodularity
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 19 September 2022, pp. 68-84
- Print publication:
- March 2023
-
- Article
- Export citation
CENTRAL LIMIT THEORY FOR COMBINED CROSS SECTION AND TIME SERIES WITH AN APPLICATION TO AGGREGATE PRODUCTIVITY SHOCKS
-
- Journal:
- Econometric Theory / Volume 40 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 19 September 2022, pp. 162-212
-
- Article
-
- You have access
- Open access
- Export citation
Negative attitudes toward older adults: Subjective time to become older and “stereotype embodiment theory”-based intervention
-
- Journal:
- Experimental Results / Volume 3 / 2022
- Published online by Cambridge University Press:
- 19 September 2022, e21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the study of the running maximum and minimum level of level-dependent quasi-birth–death processes and related models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 19 September 2022, pp. 14-29
- Print publication:
- March 2023
-
- Article
- Export citation
All that glitters is not gold: Relational events models with spurious events
-
- Journal:
- Network Science / Volume 11 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 16 September 2022, pp. 184-204
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bayesian assessments of aeroengine performance with transfer learning
-
- Journal:
- Data-Centric Engineering / Volume 3 / 2022
- Published online by Cambridge University Press:
- 15 September 2022, e29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Limit theory for U-statistics under geometric and topological constraints with rare events
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 14 September 2022, pp. 314-340
- Print publication:
- March 2023
-
- Article
- Export citation
Trajectory design via unsupervised probabilistic learning on optimal manifolds – Corrigendum
-
- Journal:
- Data-Centric Engineering / Volume 3 / 2022
- Published online by Cambridge University Press:
- 14 September 2022, e28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Block dense weighted networks with augmented degree correction
-
- Journal:
- Network Science / Volume 10 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 14 September 2022, pp. 301-321
-
- Article
- Export citation
Strong and weak tie homophily in adolescent friendship networks: An analysis of same-race and same-gender ties
-
- Journal:
- Network Science / Volume 10 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 14 September 2022, pp. 283-300
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The impact of meteorological factors and PM2.5 on COVID-19 transmission – CORRIGENDUM
-
- Journal:
- Epidemiology & Infection / Volume 150 / 2022
- Published online by Cambridge University Press:
- 14 September 2022, e164
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimal stopping under g-Expectation with
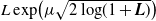 ${L}\exp\bigl(\mu\sqrt{2\log\!(1+\textbf{L})}\bigr)$-integrable reward process
${L}\exp\bigl(\mu\sqrt{2\log\!(1+\textbf{L})}\bigr)$-integrable reward process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 14 September 2022, pp. 241-252
- Print publication:
- March 2023
-
- Article
- Export citation
Caprylate/chromatography process to produce highly purified tetanus immune globulin from human plasma
-
- Journal:
- Epidemiology & Infection / Volume 150 / 2022
- Published online by Cambridge University Press:
- 13 September 2022, e172
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Critical cluster cascades
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 13 September 2022, pp. 357-381
- Print publication:
- June 2023
-
- Article
- Export citation
Evaluation of seed morphology, seedling genetic variation, and components for seed storage of Agave landraces of commercial interest
-
- Journal:
- Experimental Results / Volume 3 / 2022
- Published online by Cambridge University Press:
- 13 September 2022, e25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
How teams adapt to exogenous shocks: Experimental evidence with node knockouts of central members
-
- Journal:
- Network Science / Volume 10 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 13 September 2022, pp. 261-282
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Relaxation of the parameter independence assumption in the bootComb R package
-
- Journal:
- Experimental Results / Volume 4 / 2023
- Published online by Cambridge University Press:
- 13 September 2022, e1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Full classification of dynamics for one-dimensional continuous-time Markov chains with polynomial transition rates
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 12 September 2022, pp. 321-355
- Print publication:
- March 2023
-
- Article
- Export citation