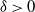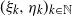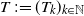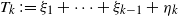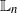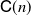Refine search
Actions for selected content:
52379 results in Statistics and Probability
Validity testing of the conspiratorial thinking and anti-expert sentiment scales during the COVID-19 pandemic across 24 languages from a large-scale global dataset
-
- Journal:
- Epidemiology & Infection / Volume 150 / 2022
- Published online by Cambridge University Press:
- 12 September 2022, e167
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Measles epidemic in Southern Vietnam: an age-stratified spatio-temporal model for infectious disease counts
-
- Journal:
- Epidemiology & Infection / Volume 150 / 2022
- Published online by Cambridge University Press:
- 12 September 2022, e169
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A machine learning algorithm to analyse the effects of vaccination on COVID-19 mortality
-
- Journal:
- Epidemiology & Infection / Volume 150 / 2022
- Published online by Cambridge University Press:
- 12 September 2022, e168
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Social clustering of unvaccinated children in schools in the Netherlands
-
- Journal:
- Epidemiology & Infection / Volume 150 / 2022
- Published online by Cambridge University Press:
- 12 September 2022, e200
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Insurers’ hidden risk from reinsurance recaptures
-
- Journal:
- British Actuarial Journal / Volume 27 / 2022
- Published online by Cambridge University Press:
- 09 September 2022, e19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Nonparametric estimation of some dividend problems in the perturbed compound Poisson model
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 37 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 09 September 2022, pp. 418-441
-
- Article
-
- You have access
- HTML
- Export citation
Optimal multiple stopping problem under nonlinear expectation
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 08 September 2022, pp. 151-178
- Print publication:
- March 2023
-
- Article
- Export citation
On improved fail-safe sensor distributions for a structural health monitoring system
- Part of
-
- Journal:
- Data-Centric Engineering / Volume 3 / 2022
- Published online by Cambridge University Press:
- 07 September 2022, e27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Uniqueness of the Gibbs measure for the 4-state anti-ferromagnetic Potts model on the regular tree
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 07 September 2022, pp. 158-182
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Connectivity-preserving distributed algorithms for removing links in directed networks
-
- Journal:
- Network Science / Volume 10 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 06 September 2022, pp. 215-233
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A journey toward an open data culture through transformation of shared data into a data resource
-
- Journal:
- Data & Policy / Volume 4 / 2022
- Published online by Cambridge University Press:
- 06 September 2022, e29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On connectivity and robustness of random graphs with inhomogeneity
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 05 September 2022, pp. 284-294
- Print publication:
- March 2023
-
- Article
- Export citation
Application of offset estimator of differential entropy and mutual information with multivariate data
-
- Journal:
- Experimental Results / Volume 3 / 2022
- Published online by Cambridge University Press:
- 05 September 2022, e16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Matrix calculations for moments of Markov processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 02 September 2022, pp. 126-150
- Print publication:
- March 2023
-
- Article
- Export citation
Fast mixing of a randomized shift-register Markov chain
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 02 September 2022, pp. 253-266
- Print publication:
- March 2023
-
- Article
- Export citation
Renewal theory for iterated perturbed random walks on a general branching process tree: Early generations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 02 September 2022, pp. 45-67
- Print publication:
- March 2023
-
- Article
- Export citation
An adjacent-swap Markov chain on coalescent trees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 02 September 2022, pp. 1243-1260
- Print publication:
- December 2022
-
- Article
- Export citation
Log-normalization constant estimation using the ensemble Kalman–Bucy filter with application to high-dimensional models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 02 September 2022, pp. 1139-1163
- Print publication:
- December 2022
-
- Article
- Export citation
Supporting peace negotiations in the Yemen war through machine learning
-
- Journal:
- Data & Policy / Volume 4 / 2022
- Published online by Cambridge University Press:
- 02 September 2022, e28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On q-scale functions of spectrally negative Lévy processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 02 September 2022, pp. 56-84
- Print publication:
- March 2023
-
- Article
- Export citation