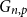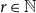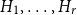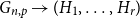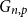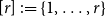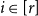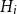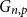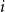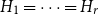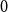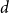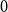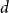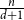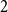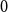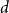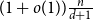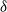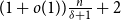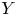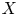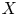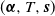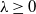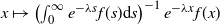Refine search
Actions for selected content:
52379 results in Statistics and Probability
Microdata collection and openness in the Middle East and North Africa
-
- Journal:
- Data & Policy / Volume 4 / 2022
- Published online by Cambridge University Press:
- 28 September 2022, e31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A new approach to impact case study analytics
-
- Journal:
- Data & Policy / Volume 4 / 2022
- Published online by Cambridge University Press:
- 28 September 2022, e30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A multi-purposed unsupervised framework for comparing embeddings of undirected and directed graphs
-
- Journal:
- Network Science / Volume 10 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 28 September 2022, pp. 323-346
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Transmission roles of symptomatic and asymptomatic COVID-19 cases: a modelling study
-
- Journal:
- Epidemiology & Infection / Volume 150 / 2022
- Published online by Cambridge University Press:
- 27 September 2022, e171
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Towards the 0-statement of the Kohayakawa-Kreuter conjecture
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 27 September 2022, pp. 225-268
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
How best to improve upon return-to-player information in gambling? A comparison of two approaches in an Australian sample
-
- Journal:
- Experimental Results / Volume 3 / 2022
- Published online by Cambridge University Press:
- 27 September 2022, e20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Large-scale behavior of a particle system with mean-field interaction: Traveling wave solutions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 27 September 2022, pp. 245-274
- Print publication:
- March 2023
-
- Article
- Export citation
Potential interactions between metal-based phenanthroline drugs and the unfolded protein response endoplasmic reticulum stress pathway
-
- Journal:
- Experimental Results / Volume 3 / 2022
- Published online by Cambridge University Press:
- 26 September 2022, e22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Panjer class revisited: one formula for the distributions of the Panjer (a,b,n) class
-
- Journal:
- Annals of Actuarial Science / Volume 17 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 26 September 2022, pp. 145-169
-
- Article
- Export citation
Convergence of the Kiefer–Wolfowitz algorithm in the presence of discontinuities
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 23 September 2022, pp. 382-406
- Print publication:
- June 2023
-
- Article
- Export citation
NWS volume 10 issue 3 Cover and Front matter
-
- Journal:
- Network Science / Volume 10 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 23 September 2022, pp. f1-f3
-
- Article
-
- You have access
- Export citation
Burden of multidrug and extensively drug-resistant ESKAPEE pathogens in a secondary hospital care setting in Greece
-
- Journal:
- Epidemiology & Infection / Volume 150 / 2022
- Published online by Cambridge University Press:
- 23 September 2022, e170
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Irregular subgraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 23 September 2022, pp. 269-283
-
- Article
- Export citation
Extreme Behaviors of the Tail Gini-Type Variability Measures
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 37 / Issue 4 / October 2023
- Published online by Cambridge University Press:
- 23 September 2022, pp. 928-942
-
- Article
- Export citation
Interacting urns on a finite directed graph
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 23 September 2022, pp. 166-188
- Print publication:
- March 2023
-
- Article
- Export citation
Preservation properties of some reliability classes by lifetimes of coherent and mixed systems and their signatures
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 37 / Issue 4 / October 2023
- Published online by Cambridge University Press:
- 23 September 2022, pp. 943-960
-
- Article
- Export citation

Principles of Data Assimilation
-
- Published online:
- 22 September 2022
- Print publication:
- 29 September 2022
Nonlinear Markov chains with finite state space: invariant distributions and long-term behaviour
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 22 September 2022, pp. 30-44
- Print publication:
- March 2023
-
- Article
- Export citation
Renal, cardiac, neurological, cutaneous and coagulopathic long-term manifestations of COVID-19 after recovery; A review
-
- Journal:
- Epidemiology & Infection / Volume 150 / 2022
- Published online by Cambridge University Press:
- 21 September 2022, e208
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A Markov jump process associated with the matrix-exponential distribution
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 20 September 2022, pp. 1-13
- Print publication:
- March 2023
-
- Article
- Export citation