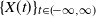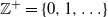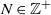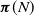Refine search
Actions for selected content:
52383 results in Statistics and Probability
Corrigendumto: Asymptotic shape and the speed of propagation of continuous-time continuous-space birth processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 03 December 2020, pp. 1325-1327
- Print publication:
- December 2020
-
- Article
-
- You have access
- HTML
- Export citation
Characterization of the conditional stationary distribution in Markov chains via systems of linear inequalities
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 03 December 2020, pp. 1249-1283
- Print publication:
- December 2020
-
- Article
- Export citation
Towards simulating a realistic data analysis with an optimised angular power spectrum of spectroscopic galaxy surveys
-
- Journal:
- Experimental Results / Volume 1 / 2020
- Published online by Cambridge University Press:
- 01 December 2020, e54
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
High MERS-CoV seropositivity associated with camel herd profile, husbandry practices and household socio-demographic characteristics in Northern Kenya
-
- Journal:
- Epidemiology & Infection / Volume 148 / 2020
- Published online by Cambridge University Press:
- 01 December 2020, e292
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A Bayesian sequential test for the drift of a fractional Brownian motion
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 03 December 2020, pp. 1308-1324
- Print publication:
- December 2020
-
- Article
- Export citation
Exact simulation for multivariate Itô diffusions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 03 December 2020, pp. 1003-1034
- Print publication:
- December 2020
-
- Article
- Export citation
Limit theorems for assortativity and clustering in null models for scale-free networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 03 December 2020, pp. 1035-1084
- Print publication:
- December 2020
-
- Article
- Export citation
COVID-19 mortality in an area of northeast Brazil: epidemiological characteristics and prospective spatiotemporal modelling
-
- Journal:
- Epidemiology & Infection / Volume 148 / 2020
- Published online by Cambridge University Press:
- 01 December 2020, e288
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On component failure in coherent systems with applications to maintenance strategies
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 03 December 2020, pp. 1197-1223
- Print publication:
- December 2020
-
- Article
- Export citation
APR volume 52 issue 4 Cover and Back matter
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 03 December 2020, pp. b1-b2
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
Asymptotic variance of Newton–Cotes quadratures based on randomized sampling points
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 03 December 2020, pp. 1284-1307
- Print publication:
- December 2020
-
- Article
- Export citation
Geometric functionals of fractal percolation
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 03 December 2020, pp. 1085-1126
- Print publication:
- December 2020
-
- Article
- Export citation
Draw-down Parisian ruin for spectrally negative Lévy processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 03 December 2020, pp. 1164-1196
- Print publication:
- December 2020
-
- Article
- Export citation

Generators of Markov Chains
- From a Walk in the Interior to a Dance on the Boundary
-
- Published online:
- 27 November 2020
- Print publication:
- 26 November 2020
Artificial intelligence for political decision-making in the European Union: Effects on citizens’ perceptions of input, throughput, and output legitimacy
-
- Journal:
- Data & Policy / Volume 2 / 2020
- Published online by Cambridge University Press:
- 27 November 2020, e16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Construction with digital twin information systems
-
- Journal:
- Data-Centric Engineering / Volume 1 / 2020
- Published online by Cambridge University Press:
- 27 November 2020, e14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
2 - Generators versus Intensity Matrices
-
- Book:
- Generators of Markov Chains
- Published online:
- 27 November 2020
- Print publication:
- 26 November 2020, pp 39-88
-
- Chapter
- Export citation
Preface
-
- Book:
- Generators of Markov Chains
- Published online:
- 27 November 2020
- Print publication:
- 26 November 2020, pp xi-xiv
-
- Chapter
- Export citation
Solutions and Hints to Selected Exercises
-
- Book:
- Generators of Markov Chains
- Published online:
- 27 November 2020
- Print publication:
- 26 November 2020, pp 245-249
-
- Chapter
- Export citation
Commonly Used Notation
-
- Book:
- Generators of Markov Chains
- Published online:
- 27 November 2020
- Print publication:
- 26 November 2020, pp 250-251
-
- Chapter
- Export citation