Determining the factors that impact the risk for infection with SARS-CoV-2 is a priority as the virus continues to infect people worldwide. The objective was to determine the effectiveness of vaccines and other factors associated with infection among Canadian healthcare workers (HCWs) followed from 15 June 2020 to 1 December 2023. We also investigate the association between antibodies to SARS-CoV-2 and subsequent infections with SARS-CoV-2. Of the 2474 eligible participants, 2133 (86%) were female, 33% were nurses, the median age was 41 years, and 99.3% had received at least two doses of COVID-19 vaccine by 31 December 2021. The incidence of SARS-CoV-2 was 0.91 per 1000 person-days. Prior to the circulation of the Omicron variants, vaccine effectiveness (VE) was estimated at 85% (95% CI 1, 98) for participants who received the primary series of vaccine. During the Omicron period, relative adjusted VE was 43% (95% CI 29, 54), 56% (95% CI 42, 67), and 46% (95% CI 24, 62) for 3, 4, and ≥ 5 doses compared with those who received primary series after adjusting for previous infection and other covariates. Exposure to infected household members, coworkers, or friends in the previous 14 days were risk factor for infection, while contact with an infected patient was not statistically significant. Participants with higher levels of immunoglobulin G (IgG) anti-receptor binding domain (RBD) antibodies had lower rates of infection than those with the lowest levels. COVID-19 vaccines remained effective throughout the follow-up of this cohort of highly vaccinated HCWs. IgG anti-RBD antibody levels may be useful as correlates of protection for issues such as vaccine development and testing. There remains a need to increase the awareness among HCWs about the risk of contracting SARS-CoV-2 from contacts at a variety of venues.

Actuaries must model mortality to understand, manage and price risk. Continuous-time methods offer considerable practical benefits to actuaries analysing portfolio mortality experience. This paper discusses six categories of advantage: (i) reflecting the reality of data produced by everyday business practices, (ii) modelling rapid changes in risk, (iii) modelling time- and duration-varying risk, (iv) competing risks, (v) data-quality checking and (vi) management information. Specific examples are given where continuous-time models are more useful in practice than discrete-time models.

Competing and complementary risk (CCR) problems are often modelled using a class of distributions of the maximum, or minimum, of a random number of independent and identically distributed random variables, called the CCR class of distributions. While CCR distributions generally do not have an easy-to-calculate density or probability mass function, two special cases, namely the Poisson–exponential and exponential–geometric distributions, can easily be calculated. Hence, it is of interest to approximate CCR distributions with these simpler distributions. In this paper, we develop Stein’s method for the CCR class of distributions to provide a general comparison method for bounding the distance between two CCR distributions, and we contrast this approach with bounds obtained using a Lindeberg argument. We detail the comparisons for Poisson–exponential, and exponential–geometric distributions.

We reprise some common statistical models for actuarial mortality analysis using grouped counts. We then discuss the benefits of building mortality models from the most elementary items. This has two facets. First, models are better based on the mortality of individuals, rather than groups. Second, models are better defined in continuous time, rather than over fixed intervals like a year. We show how Poisson-like likelihoods at the “macro” level are built up by product integration of sequences of infinitesimal Bernoulli trials at the “micro” level. Observed data is represented through a stochastic mortality hazard rate, and counting processes provide the natural notation for left-truncated and right-censored actuarial data, individual or age-grouped. Together these explain the “pseudo-Poisson” behaviour of survival model likelihoods.

Stochastic actor-oriented models (SAOMs) were designed in the social network setting to capture network dynamics representing a variety of influences on network change. The standard framework assumes the observed networks are free of false positive and false negative edges, which may be an unrealistic assumption. We propose a hidden Markov model (HMM) extension to these models, consisting of two components: 1) a latent model, which assumes that the unobserved, true networks evolve according to a Markov process as they do in the SAOM framework; and 2) a measurement model, which describes the conditional distribution of the observed networks given the true networks. An expectation-maximization algorithm is developed for parameter estimation. We address the computational challenge posed by a massive discrete state space, of a size exponentially increasing in the number of vertices, through the use of the missing information principle and particle filtering. We present results from a simulation study, demonstrating our approach offers improvement in accuracy of estimation, in contrast to the standard SAOM, when the underlying networks are observed with noise. We apply our method to functional brain networks inferred from electroencephalogram data, revealing larger effect sizes when compared to the naive approach of fitting the standard SAOM.

This systematic review synthesized evidence on the viral load of severe acute respiratory syndrome coronavirus-2 (SARS-CoV-2) shedding in exhaled material to understand how the exhaled SARS-CoV-2 viral load of infected individuals varies with days since exposure. Medline, Scopus, and Web of Science databases were searched using a combination of search terms to identify articles that tested exhaled material from SARS-CoV-2 infected patients. Records were systematically screened and assessed for eligibility, following which reference lists of eligible articles were hand-searched to identify further relevant studies. Data extraction and quality assessment of individual studies were conducted prior to synthesizing the evidence. Forty-five articles that sampled exhaled breath, exhaled breath condensate, face masks, and cough samples were reviewed. The variation in the SARS-CoV-2 viral load in these materials was considerable with the detection of viral RNA shed during breathing as far as 43 days after symptom onset. The replication-competent virus was present in all four sample types, with the majority isolated during the first week of symptoms onset. Variations in the sample types and testing protocols precluded meta-analysis. High heterogeneity in exhaled SARS-CoV-2 viral load is likely due to host and viral factors as well as variations in sampling and diagnostic methodologies. Evidence on SARS-CoV-2 shedding in exhaled material is scarce and more controlled fundamental studies are needed to assess this important route of viral shedding.

The classical credibility premium provides a simple and efficient method for predicting future damages and losses. However, when dealing with a nonhomogeneous population, this widely used technique has been challenged by the Regression Tree Credibility (RTC) model and the Logistic Regression Credibility (LRC) model. This article introduces the Mixture Credibility Formula (MCF), which represents a convex combination of the classical credibility premiums of several homogeneous subpopulations derived from the original population. We also compare the performance of the MCF method with the RTC and LRC methods. Our analysis demonstrates that the MCF method consistently outperforms these approaches in terms of the quadratic loss function, highlighting its effectiveness in refining insurance premium calculations and enhancing risk assessment strategies.

We consider stationary configurations of points in Euclidean space that are marked by positive random variables called scores. The scores are allowed to depend on the relative positions of other points and outside sources of randomness. Such models have been thoroughly studied in stochastic geometry, e.g. in the context of random tessellations or random geometric graphs. It turns out that in a neighborhood of a point with an extreme score it is possible to rescale positions and scores of nearby points to obtain a limiting point process, which we call the tail configuration. Under some assumptions on dependence between scores, this local limit determines the global asymptotics for extreme scores within increasing windows in $\mathbb{R}^d$. The main result establishes the convergence of rescaled positions and clusters of high scores to a Poisson cluster process, quantifying the idea of the Poisson clumping heuristic by Aldous (1989, in the point process setting). In contrast to the existing results, our framework allows for explicit calculation of essentially all extremal quantities related to the limiting behavior of extremes. We apply our results to models based on (marked) Poisson processes where the scores depend on the distance to the kth nearest neighbor and where scores are allowed to propagate through a random network of points depending on their locations.

Simulations of critical phenomena, such as wildfires, epidemics, and ocean dynamics, are indispensable tools for decision-making. Many of these simulations are based on models expressed as Partial Differential Equations (PDEs). PDEs are invaluable inductive inference engines, as their solutions generalize beyond the particular problems they describe. Methods and insights acquired by solving the Navier–Stokes equations for turbulence can be very useful in tackling the Black-Scholes equations in finance. Advances in numerical methods, algorithms, software, and hardware over the last 60 years have enabled simulation frontiers that were unimaginable a couple of decades ago. However, there are increasing concerns that such advances are not sustainable. The energy demands of computers are soaring, while the availability of vast amounts of data and Machine Learning(ML) techniques are challenging classical methods of inference and even the need of PDE based forecasting of complex systems. I believe that the relationship between ML and PDEs needs to be reset. PDEs are not the only answer to modeling and ML is not necessarily a replacement, but a potent companion of human thinking. Algorithmic alloys of scientific computing and ML present a disruptive potential for the reliable and robust forecasting of complex systems. In order to achieve these advances, we argue for a rigorous assessment of their relative merits and drawbacks and the adoption of probabilistic thinking for developing complementary concepts between ML and scientific computing. The convergence of AI and scientific computing opens new horizons for scientific discovery and effective decision-making.

We study convergence rates, in mean, for the Hausdorff metric between a finite set of stationary random variables and their common support, which is supposed to be a compact subset of $\mathbb{R}^d$. We propose two different approaches for this study. The first is based on the notion of a minimal index. This notion is introduced in this paper. It is in the spirit of the extremal index, which is much used in extreme value theory. The second approach is based on a $\beta$-mixing condition together with a local-type dependence assumption. More precisely, all our results concern stationary $\beta$-mixing sequences satisfying a tail condition, known as the (a, b)-standard assumption, together with a local-type dependence condition or stationary sequences satisfying the (a, b)-standard assumption and having a positive minimal index. We prove that the optimal rates of the independent and identically distributed setting can be reached. We apply our results to stationary Markov chains on a ball, or to a class of Markov chains on a circle or on a torus. We study with simulations the particular examples of a Möbius Markov chain on the unit circle and of a Markov chain on the unit square wrapped on a torus.

Previously, we reported the persistence of the bacterial pathogen Neisseria meningitidis on fomites, indicating a potential route for environmental transmission. The current goal was to identify proteins that vary among strains of meningococci that have differing environmental survival. We carried out a proteomic analysis of two strains that differ in their potential for survival outside the host. The Group B epidemic strain NZ98/254 and Group W carriage strain H34 were cultured either at 36 °C, 5% CO2, and 95% relative humidity (RH) corresponding to host conditions in the nasopharynx, or at lower humidities of 22% or 30% RH at 30 °C, for which there was greater survival on fomites. For NZ98/254, the shift to lower RH and temperature was associated with increased abundance of proteins involved in metabolism, stress responses, and outer membrane components, including pili and porins. In contrast, H34 responded to lower RH by decreasing the abundance of multiple proteins, indicating that the lower viability of H34 may be linked to decreased capacity to mount core protective responses. The results provide a snapshot of bacterial proteins and metabolism that may be related to normal fitness, to the greater environmental persistence of NZ98/254 compared to H34, and potentially to differences in transmission and pathogenicity.

This work concerns stochastic differential equations with jumps. We prove convergence for solutions to a sequence of (possibly degenerate) stochastic differential equations with jumps when the coefficients converge in some appropriate sense. Then some special cases are analyzed and some concrete and verifiable conditions are given.

This article studies the robustness of quasi-maximum-likelihood estimation in hidden Markov models when the regime-switching structure is misspecified. Specifically, we examine the case where the data-generating process features a hidden Markov regime sequence with covariate-dependent transition probabilities, but estimation proceeds under a simplified mixture model that assumes regimes are independent and identically distributed. We show that the parameters governing the conditional distribution of the observables can still be consistently estimated under this misspecification, provided certain regularity conditions hold. Our results highlight a practical benefit of using computationally simpler mixture models in settings where regime dependence is complex or difficult to model directly.

We develop explicit bounds for the tail of the distribution of the all-time supremum of a random walk with negative drift, where the increments have a truncated heavy-tailed distribution. As an application, we consider a ruin problem in the presence of reinsurance.

We study the uniform convergence rates of nonparametric estimators for a probability density function and its derivatives when the density has a known pole. Such situations arise in some structural microeconometric models, for example, in auction, labor, and consumer search, where uniform convergence rates of density functions are important for nonparametric and semiparametric estimation. Existing uniform convergence rates based on Rosenblatt’s kernel estimator are derived under the assumption that the density is bounded. They are not applicable when there is a pole in the density. We treat the pole nonparametrically and show various kernel-based estimators can attain any convergence rate that is slower than the optimal rate when the density is bounded uniformly over an appropriately expanding support under mild conditions.

We investigate geometric properties of invariant spatio-temporal random fields $X\colon\mathbb M^d\times \mathbb R\to \mathbb R$ defined on a compact two-point homogeneous space $\mathbb M^d$ in any dimension $d\ge 2$, and evolving over time. In particular, we focus on chi-squared-distributed random fields, and study the large-time behavior (as $T\to +\infty$) of the average on [0,T] of the volume of the excursion set on the manifold, i.e. of $\lbrace X(\cdot, t)\ge u\rbrace$ (for any $u >0$). The Fourier components of X may have short or long memory in time, i.e. integrable or non-integrable temporal covariance functions. Our argument follows the approach developed in Marinucci et al. 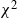(2021) and allows us to extend their results for invariant spatio-temporal Gaussian fields on the two-dimensional unit sphere to the case of chi-squared distributed fields on two-point homogeneous spaces in any dimension. We find that both the asymptotic variance and limiting distribution, as $T\to +\infty$, of the average empirical volume turn out to be non-universal, depending on the memory parameters of the field X.

The efficient integration of outpatient (OPD) and inpatient (IPD) care is a critical challenge in modern healthcare, essential for maximising patient-centred care and resource utilisation. OPD, encompassing preventive services, routine check-ups, and chronic disease management, aims to minimise the need for hospitalisations. Conversely, IPD remains crucial for acute interventions and complex medical needs. This paper investigates the nuanced relationship between OPD and IPD: specifically, we seek to determine if increased OPD utilisation while improving overall health, leads to a reduction or increase in subsequent IPD utilisation, duration, and associated costs. We analyse anonymised data from Indian organisations providing company-sponsored OPD and IPD insurance to their employees between 2021 and 2024. By examining the correlation between OPD utilisation patterns and IPD outcomes, we aim to provide data-driven insights for effective healthcare integration strategies. Furthermore, we explore the feasibility of developing a personalised “Wellbeing Rating” derived from longitudinal OPD insurance utilisation data. This automated methodology aims to provide a continuous, dynamic health assessment, moving beyond the limitations of traditional, sporadic medical examinations by leveraging the comprehensive data inherent within insured OPD coverage.