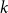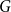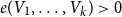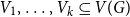Refine search
Actions for selected content:
52346 results in Statistics and Probability
Part III - Fighting Nonignorable Nonresponse
-
- Book:
- Polling at a Crossroads
- Published online:
- 29 February 2024
- Print publication:
- 07 March 2024, pp 135-136
-
- Chapter
- Export citation
1 - Modern Polling
- from Part I - Polling in Context
-
- Book:
- Polling at a Crossroads
- Published online:
- 29 February 2024
- Print publication:
- 07 March 2024, pp 3-22
-
- Chapter
-
- You have access
- Export citation
Part IV - Applications
-
- Book:
- Polling at a Crossroads
- Published online:
- 29 February 2024
- Print publication:
- 07 March 2024, pp 211-212
-
- Chapter
- Export citation
10 - Randomized Response Instruments
- from Part III - Fighting Nonignorable Nonresponse
-
- Book:
- Polling at a Crossroads
- Published online:
- 29 February 2024
- Print publication:
- 07 March 2024, pp 183-197
-
- Chapter
- Export citation
A NONPARAMETRIC TEST OF HETEROGENEITY IN CONDITIONAL QUANTILE TREATMENT EFFECTS
-
- Journal:
- Econometric Theory / Volume 41 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 07 March 2024, pp. 660-687
-
- Article
-
- You have access
- Open access
- Export citation
Acknowledgments
-
- Book:
- Polling at a Crossroads
- Published online:
- 29 February 2024
- Print publication:
- 07 March 2024, pp xix-xx
-
- Chapter
- Export citation
Skew Ornstein–Uhlenbeck processes with sticky reflection and their applications to bond pricing
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 06 March 2024, pp. 1172-1195
- Print publication:
- December 2024
-
- Article
- Export citation
Antidirected subgraphs of oriented graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 06 March 2024, pp. 446-466
-
- Article
- Export citation
Large monochromatic components in expansive hypergraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 05 March 2024, pp. 467-483
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A class of graphs of zero Turán density in a hypercube
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 05 March 2024, pp. 404-410
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Some properties of convex and increasing convex orders under Archimedean copula
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 4 / October 2024
- Published online by Cambridge University Press:
- 05 March 2024, pp. 632-643
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sharp bounds for a discrete John’s theorem
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 05 March 2024, pp. 484-486
-
- Article
- Export citation
COVID-19 outbreak at a residential apartment building in Northern Ontario, Canada
-
- Journal:
- Epidemiology & Infection / Volume 152 / 2024
- Published online by Cambridge University Press:
- 04 March 2024, e53
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Perfect sampling of stochastic matching models with reneging
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 04 March 2024, pp. 1307-1339
- Print publication:
- December 2024
-
- Article
-
- You have access
- HTML
- Export citation
Post-migration HIV acquisition: A systematic review and meta-analysis
-
- Journal:
- Epidemiology & Infection / Volume 152 / 2024
- Published online by Cambridge University Press:
- 01 March 2024, e49
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
When data meets citizens: an investigation of citizen engagement in data-driven innovation programmes
-
- Journal:
- Data & Policy / Volume 6 / 2024
- Published online by Cambridge University Press:
- 01 March 2024, e12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Heavy-traffic queue length behavior in a switch under Markovian arrivals
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 01 March 2024, pp. 1106-1152
- Print publication:
- September 2024
-
- Article
-
- You have access
- HTML
- Export citation

Polling at a Crossroads
- Rethinking Modern Survey Research
-
- Published online:
- 29 February 2024
- Print publication:
- 07 March 2024
2 - How Are Subscores Reported?
-
- Book:
- Subscores
- Published online:
- 22 February 2024
- Print publication:
- 29 February 2024, pp 18-44
-
- Chapter
- Export citation
7 - Statistical Boosting for GAMLSS
- from Part II - Statistical Inference in GAMLSS
-
- Book:
- Generalized Additive Models for Location, Scale and Shape
- Published online:
- 22 February 2024
- Print publication:
- 29 February 2024, pp 165-194
-
- Chapter
- Export citation