We prove the existence and give constructions of a 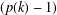 $(p(k)-1)$ -fold perfect resolvable
$(p(k)-1)$ -fold perfect resolvable 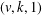 $(v,k,1)$ -Mendelsohn design for any integers
$(v,k,1)$ -Mendelsohn design for any integers 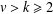 $v>k\geq 2$ with
$v>k\geq 2$ with 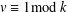 $v\equiv 1\hspace{0.2em}{\rm mod}\hspace{0.2em}\,k$ such that there exists a finite Frobenius group whose kernel
$v\equiv 1\hspace{0.2em}{\rm mod}\hspace{0.2em}\,k$ such that there exists a finite Frobenius group whose kernel 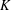 $K$ has order
$K$ has order  $v$ and whose complement contains an element
$v$ and whose complement contains an element 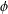 $\unicode[STIX]{x1D719}$ of order
$\unicode[STIX]{x1D719}$ of order 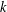 $k$ , where
$k$ , where 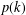 $p(k)$ is the least prime factor of
$p(k)$ is the least prime factor of 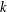 $k$ . Such a design admits
$k$ . Such a design admits 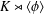 $K\rtimes \langle \unicode[STIX]{x1D719}\rangle$ as a group of automorphisms and is perfect when
$K\rtimes \langle \unicode[STIX]{x1D719}\rangle$ as a group of automorphisms and is perfect when 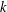 $k$ is a prime. As an application we prove that for any integer
$k$ is a prime. As an application we prove that for any integer 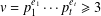 $v=p_{1}^{e_{1}}\cdots p_{t}^{e_{t}}\geq 3$ in prime factorisation and any prime
$v=p_{1}^{e_{1}}\cdots p_{t}^{e_{t}}\geq 3$ in prime factorisation and any prime 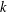 $k$ dividing
$k$ dividing 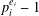 $p_{i}^{e_{i}}-1$ for
$p_{i}^{e_{i}}-1$ for 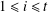 $1\leq i\leq t$ , there exists a resolvable perfect
$1\leq i\leq t$ , there exists a resolvable perfect 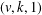 $(v,k,1)$ -Mendelsohn design that admits a Frobenius group as a group of automorphisms. We also prove that, if
$(v,k,1)$ -Mendelsohn design that admits a Frobenius group as a group of automorphisms. We also prove that, if 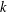 $k$ is even and divides
$k$ is even and divides 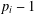 $p_{i}-1$ for
$p_{i}-1$ for 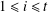 $1\leq i\leq t$ , then there are at least
$1\leq i\leq t$ , then there are at least 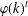 $\unicode[STIX]{x1D711}(k)^{t}$ resolvable
$\unicode[STIX]{x1D711}(k)^{t}$ resolvable 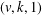 $(v,k,1)$ -Mendelsohn designs that admit a Frobenius group as a group of automorphisms, where
$(v,k,1)$ -Mendelsohn designs that admit a Frobenius group as a group of automorphisms, where 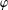 $\unicode[STIX]{x1D711}$ is Euler’s totient function.
$\unicode[STIX]{x1D711}$ is Euler’s totient function.
 $p$ -ADIC GAMMA FUNCTIONS
$p$ -ADIC GAMMA FUNCTIONS
 $\unicode[STIX]{x1D705}$ ) SPACES
$\unicode[STIX]{x1D705}$ ) SPACES
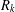 $R_{k}$
$R_{k}$