It is well known that in a separable topological space every point-finite family of open subsets is countable. In the following we are going to show that both in σ-finite measure-spaces and in topological spaces satisfying the countable chain condition, point-finite families consisting of “large” subsets are countable.

Notation and terminology. Let A be a set. The family consisting of all (finite) subsets of A is denoted by . Let be a family of subsets of A. The sets and are denoted by and , respectively. We say that the family is point-finite (disjoint) if for each a ∈ A , the family has at most finitely many members (at most one member).

The geometry of Hjelmslev groups is a comprehensive plane metric geometry. It supplies, for example, an approach to euclidean, hyperbolic, elliptic, Minkowskian and Galilean geometry.

The subject of this geometry are Hjelmslev groups and their group planes. (The definition of Hjelmslev groups and some basic concepts and propositions of this theory can be found in the second edition of Bachmann's book [1] (pages 318-328). A similar report in English is the lecture [3]. A comprehensive introduction is developed in the key work [2]. The first part of this work was translated by Garner [4]. An abstract is given in Math. Rev. 52, 9066 (1976).) The group plane arises from giving geometric names to some group theoretical facts. The group plane of a Hjelmslev group is an incidence structure with orthogonality, and the Hjelmslev group acts on this plane as a group of motions.

The purpose of the present note is to introduce some notions useful for applications of the trace formula to the study of the principle of functoriality, including base change, and to the study of zeta-functions of Shimura varieties. In order to avoid disconcerting technical digressions I shall work with reductive groups over fields of characteristic zero, but the second assumption is only a matter of convenience, for the problems caused by inseparability are not serious.

The difficulties with which the trace formula confronts us are manifold. Most of them arise from the non-compactness of the quotient and will not concern us here. Others are primarily arithmetic and occur even when the quotient is compact. To see how they arise, we consider a typical problem.

The notion of L-indistinguishability, like many others current in the study of L-functions, has yet to be completely defined, but it is in our opinion important for the study of automorphic forms and of representations of algebraic groups. In this paper we study it for the simplest class of groups, basically forms of SL(2). Although the definition we use is applicable to very few groups, there is every reason to believe that the results will have general analogues [12].

The phenomena which the notion is intended to express have been met–and exploited–by others (Hecke [5] § 13, Shimura [17]). Their source seems to lie in the distinction between conjugacy and stable conjugacy. If F is a field, G a reductive algebraic group over F, and the algebraic closure of F then two elements of G(F) may be conjugate in without being conjugate in G(F).

We extend a theorem of L. E. Dubins on “purely finitely additive disintegrations” of measures (cf. [4]) and apply this result to the disintegrations of extremal Gibbs states with respect to the asymptotic algebra enlarging another result of L. E. Dubins on the symmetric coin tossing game.

We recall the following definition of L. E. Dubins (cf. [3], [4]): Let (X , , μ) be a measure space, a sub σ-algebra of . A real function σx (A), is called a measurable-disintegration of μ if:

• (i) ∀x ∊ X , σx(.) is a finitely additive measure .

• (ii) ∀A ∊ , σ. (A) is constant on each -atom.

• (iii) For each A ∊ , σ. (A) is measurable with respect to the completion of by μ and

• (iv) σx(B) = 1 if x ∊ B ∊ .

Noether lattices were introduced by R. P. Dilworth in [5] and constitute a natural abstraction of the lattice of ideals of a Noetherian ring. In his definitive work, Dilworth showed that a minimal prime of an element generated by n principal elements has rank ≦ n. Following standard ring theoretical terminology, a local Noether lattice with (unique) maximal element M is said to be regular if M has rank n and can be generated by n principal elements.

In [3], K. P. Bogart showed that a distributive regular local Noether lattice of Krull dimension n is isomorphic to RLn, the sublattice of all ideals generated by monomials of any polynomial ring (k a field). In a later paper [4], Bogart extended his results on distributive regular local Noether lattices by showing that any distributive local Noether lattice is the image of a multiplicative map θ which preserves joins, and can in fact be thought of as the related congruence lattice.

If X is a nonempty topological T1 space then the set of all homeomorphisms whose domains and ranges are closed subsets of X forms a semigroup under partial composition of functions. We call it IF(X). If, in a semigroup, every element a is matched with a unique element b such that aba = a and bab = b then the semigroup is an inverse semigroup (b is called the inverse of a and is denoted by a −1). We have that IF(X) is an inverse semigroup with the algebraic inverse of a map ƒ being just the inverse map ƒ -1. In this paper we examine epimorphisms from IF(X) onto IF(Y). The main theorem gives conditions under which an epimorphism must be an isomorphism.

Throughout this note, let R be a discrete valuation ring with prime element π, residue class field , and quotient field K. Let Λ be an R-order in a finite dimensional K-algebra A. A Λ-lattice is an R-free finitely generated left Λ-module. For k > 0, we set

where M is any Λ-lattice. Obviously, for Λ-lattices M and N,

Maranda [1] and D. G. Higman [3] considered the reverse implication, and Proved

THEOREM. Let Λ be an R-order in a separable K-algebra A. Then there exists a positive integer k (which depends on Λ) with the following property: for each pair of Λ-lattices M and N,

Indeed,m it suffices to choose k so that

Maranda proved this result for the special case where Λ is the integral group ring RG of a finite group G.

In a previous work [6] it was shown that by imposing certain finiteness conditions on a nilpotent loop certain algebraic results yielded properties about [X, Y] where X is finite CW and Y is an H-Space. In this sequel we further restrict the category of nilpotent loops to a full subcategory called H-loops which still contains all loops of the form [X, Y], We prove that on this category there is a unique and universal P-localization if P ≠ ∅ which corresponds to topological localization. We also show that if the H-loop is a group then the two concepts of localization agree.

The first section of this paper is devoted to the definition and basic properties of H-loops. In the second section we develop the localization construction and prove uniqueness. Finally, in the third section we consider the topological and group theoretic situations.

All topological spaces under discussion are assumed to be Tychonoff.

For any topological space X let τ(X) denote the topology of X. If X ᑕ Y then a function κ : τ(X) ⟶ τ(Y) is called an extender provided that κ(U) ∩ X = U for all U ∊ τ(X). In addition, X is said to be Kn-embedded in Y (cf. [3]) provided there is an extender κ : τ(X) ⟶ τ(Y) such that

The extender κ is called a Kn -function (cf. [3]).

Eric van Douwen has asked whether there is a space X with a subspace Z which is Ki -embedded but not K0 -embedded. The aim of this note is to answer this question.

Based on a strategy of Kaplansky ([3]), Dixmier proved that a prime, separable C*-algebra is primitive ([1]). As a consequence, when the C*-closure of a countable discrete group is prime, it is primitive. The argument may be regarded as a clever application of the Baire Category Theorem to the spectrum of irreducible representations.

The present note is the first step in adapting this technique to abstract group algebras. For which groups G is the primitive ideal space of k[G] a Baire space? One corollary of our main result is that the space is Baire when k is an uncountable field and G is a polycyclic-by-finite group. This gives an alternate proof of a special case of Passman's theorem that such a k[G] will be primitive when its center is k ([4], p. 379).

The well-known Hasse-Brauer-Noether theorem states that a simple algebra with center a number field k splits over k (i.e., is a full matrix algebra) if and only if it splits over the completion of k at every rank one valuation of k. It is natural to ask whether this principle can be extended to a broader class of fields. In particular, we prove here the following extension.

We discuss the decomposition of tensor products of holomorphic discrete series representations, generalizing a technique used in [9] for representations of SL 2(R), based on a suggestion of Roger Howe. In the case of two representations with highest weights, the discussion is entirely algebraic, and is best formulated in the context of generalized Verma modules (see § 3). In the case when one representation has a highest weight and the other a lowest weight, the approach is more analytic, relying on the realization of these representations on certain spaces of holomorphic functions.

For a simple group, these two cases exhaust the possibilities; for a nonsimple group, one has to piece together representations on the various factors.

The author wishes to thank Roger Howe and Jim Lepowsky for very helpful conversations, and Nolan Wallach for pointing out the work of Eugene Gutkin (Thesis, Brandeis University, 1978), from which some of the results of this paper can be read off as easy corollaries.

Let Aj and Bj (1 ≦ j ≦ m) be bounded operators on a Banach space ᚕ and let Φ be the mapping on , the algebra of bounded operators on ᚕ, defined by

(1)

We give necessary and sufficient conditions for Φ to be identically zero or to be a compact map or (in the Hilbert space case) for the induced mapping on the Calkin algebra to be identically zero. These results are then used to obtain some results about inner derivations and, more generally, about mappings of the form

For example, it is shown that the commutant of the range of C(S, T) is “small” unless S and T are scalars.

Let G denote the group of integers of a p-series field, where p is a prime ≦ 2. Thus, any element can be represented as a sequence {xi }i = 0 ∞ with 0 ≦ xi < p for each i ≦ 0. Moreover, the dual group {Ψm }m = 0 ∞ of G can be described by the following process. If m is a non-negative integer with for each k , and if then

(1)

where for each integer k ≧ 0 and for each x = {xi } ∈ G the functions Φk are defined by

(2)

In the case that p = 2, the group G is the dyadic group introduced by Fine [1] and the functions are the Walsh-Paley functions. A detailed account of these groups and basic properties can be found in [4].

We present an example which illustrates several peculiar phenomena that may occur in the theory of C*-algebras. In particular, we show that a C*-subalgebra of a nuclear (amenable) C*-algebra need not be nuclear (amenable).

The central object of this paper is a pair of abstract unitary matrices,

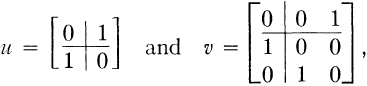
acting on a common Hilbert space. For an explicit construction, we may decompose an infinite-dimensional Hilbert space H into H = H0 ⴲ H1 , H 1 = H α ⴲ H β with dim H 0 = dim H 1 = dim H α = dim H β, letting u, v Є B(H) be any two unitary operators such that

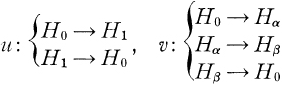
and u2 = 1, v3 = 1. Whereas many choices of u, v are possible, it might be surprising to see that C*(u, v), the C*-algebra generated by u and v, is algebraically unique; namely, if (u1,V1) is another pair of such unitaries, then C*(u, v) is canonically *-isomorphic with C*(u 1, v 1) (Theorem 2.6).

In the theory of functions of several complex variables one is naturally led to study non-compact complex manifolds which have certain types of exhaustions. For example, on a Stein manifold X there is a strictly plurisubharmonic function ϕ: X → R+ so that the pseudoballs Bc = {φ < c } exhaust X. Conversely, a manifold which has such an exhaustion is Stein. The purpose of this note is to study a class of manifolds which have exhaustions along the lines of those on holomorphically convex manifolds, namely the k-Leviflat complex manifolds. Unlike the Stein case, the Levi form may have positive dimensional 0-eigenspaces. In the holomorphically convex case these are tangent to the generic fiber of the Remmert reduction.

In this paper, X denotes a completely regular Hausdorff space, Cb(X) all real-valued bounded continuous functions on X, E a Hausforff locally convex space over reals R, Cb(X, E) all bounded continuous functions from X into E, Cb(X) ⴲ E the tensor product of Cb(X) and E. For locally convex spaces E and F, E ⴲ, F denotes the tensor product with the topology of uniform convergence on sets of the form S X T where S and T are equicontinuous subsets of E′, F′ the topological duals of E, F respectively ([11], p. 96). For a locally convex space G , G ′ will denote its topological dual.