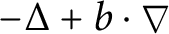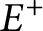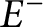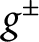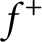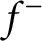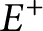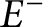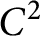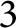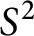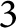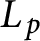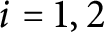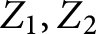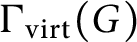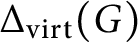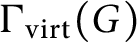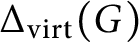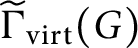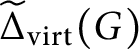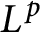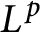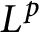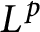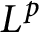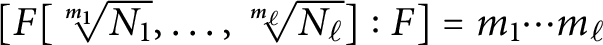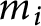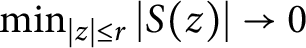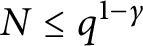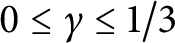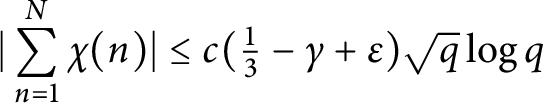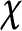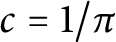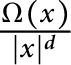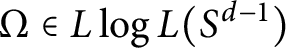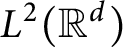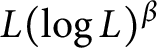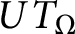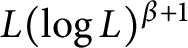Contents
Article
Regularity theory of Kolmogorov operator revisited
- Part of:
-
- Published online by Cambridge University Press:
- 24 August 2020, pp. 725-736
-
- Article
- Export citation
Optimal free export/import regions
- Part of:
-
- Published online by Cambridge University Press:
- 17 September 2020, pp. 737-751
-
- Article
- Export citation
On framings of links in 3-manifolds
- Part of:
-
- Published online by Cambridge University Press:
- 21 September 2020, pp. 752-764
-
- Article
- Export citation
Sharp affine Trudinger–Moser inequalities: A new argument
- Part of:
-
- Published online by Cambridge University Press:
- 22 October 2020, pp. 765-778
-
- Article
- Export citation
A note on the phase retrieval of holomorphic functions
- Part of:
-
- Published online by Cambridge University Press:
- 08 October 2020, pp. 779-786
-
- Article
- Export citation
Brill-Noether generality of binary curves
- Part of:
-
- Published online by Cambridge University Press:
- 13 October 2020, pp. 787-807
-
- Article
- Export citation
The virtually generating graph of a profinite group
- Part of:
-
- Published online by Cambridge University Press:
- 15 October 2020, pp. 808-819
-
- Article
- Export citation
Relations between modular invariants of a vector and a covector in dimension two
- Part of:
-
- Published online by Cambridge University Press:
- 28 October 2020, pp. 820-827
-
- Article
- Export citation
Surjective isometries of metric geometries
- Part of:
-
- Published online by Cambridge University Press:
- 28 October 2020, pp. 828-839
-
- Article
- Export citation
Autocorrelation functions for quantum particles in supersymmetric Pöschl-Teller potentials
- Part of:
-
- Published online by Cambridge University Press:
- 28 October 2020, pp. 840-852
-
- Article
- Export citation
On isomorphisms between weighted
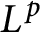 $L^p$-algebras
$L^p$-algebras
- Part of:
-
- Published online by Cambridge University Press:
- 30 October 2020, pp. 853-866
-
- Article
- Export citation
Degree gaps for multipliers and the dynamical André–Oort conjecture
- Part of:
-
- Published online by Cambridge University Press:
- 13 November 2020, pp. 867-876
-
- Article
- Export citation
On the degree of repeated radical extensions
- Part of:
-
- Published online by Cambridge University Press:
- 23 November 2020, pp. 877-885
-
- Article
- Export citation
Prescribed k-symmetric curvature hypersurfaces in de Sitter space
- Part of:
-
- Published online by Cambridge University Press:
- 26 November 2020, pp. 886-901
-
- Article
- Export citation
On the decay of singular inner functions
- Part of:
-
- Published online by Cambridge University Press:
- 02 December 2020, pp. 902-905
-
- Article
- Export citation
A Pólya–Vinogradov inequality for short character sums
- Part of:
-
- Published online by Cambridge University Press:
- 02 December 2020, pp. 906-910
-
- Article
- Export citation
An estimate for the composition of rough singular integral operators
- Part of:
-
- Published online by Cambridge University Press:
- 07 December 2020, pp. 911-922
-
- Article
- Export citation
A characterization of singular Schrödinger operators on the half-line
- Part of:
-
- Published online by Cambridge University Press:
- 07 December 2020, pp. 923-941
-
- Article
- Export citation
Tight frames and related geometric problems
- Part of:
-
- Published online by Cambridge University Press:
- 18 December 2020, pp. 942-963
-
- Article
- Export citation
Inequalities on partial traces of positive semidefinite block matrices
- Part of:
-
- Published online by Cambridge University Press:
- 18 December 2020, pp. 964-969
-
- Article
- Export citation