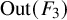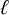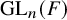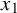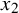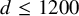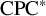Contents
Differential Geometry and Geometric Analysis
The conjugacy problem for
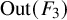 $\operatorname {Out}(F_3)$
$\operatorname {Out}(F_3)$
- Part of:
-
- Published online by Cambridge University Press:
- 13 February 2025, e41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebra
The Quantitative Kurosh Problem
- Part of:
-
- Published online by Cambridge University Press:
- 13 February 2025, e42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Number Theory
Semi-infinite orbits in affine flag varieties and homology of affine Springer fibers
-
- Published online by Cambridge University Press:
- 13 February 2025, e43
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebraic and Complex Geometry
Coordinate rings of regular nilpotent Hessenberg varieties in the open opposite schubert cell
- Part of:
-
- Published online by Cambridge University Press:
- 17 February 2025, e44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Number Theory
On local Galois deformation rings: generalised tori
- Part of:
-
- Published online by Cambridge University Press:
- 18 February 2025, e45
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Erratum
Canonical heights for abelian group actions of maximal dynamical rank - ERRATUM
-
- Published online by Cambridge University Press:
- 18 February 2025, e46
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Discrete Mathematics
A raising operator formula for Macdonald polynomials
- Part of:
-
- Published online by Cambridge University Press:
- 19 February 2025, e47
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebra
Cuspidal
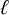 ${\ell }$-modular representations of
${\ell }$-modular representations of 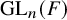 $\operatorname {GL}_n({ F})$ distinguished by a Galois involution
$\operatorname {GL}_n({ F})$ distinguished by a Galois involution
- Part of:
-
- Published online by Cambridge University Press:
- 20 February 2025, e48
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Discrete Mathematics
Sphere packings in Euclidean space with forbidden distances
-
- Published online by Cambridge University Press:
- 25 February 2025, e49
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Number Theory
Kodaira–Spencer isomorphisms and degeneracy maps on Iwahori-level Hilbert modular varieties: the saving trace
- Part of:
-
- Published online by Cambridge University Press:
- 28 February 2025, e50
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Analysis
Elliptic Pre-Complexes, Hodge-like Decompositions and Overdetermined Boundary-Value Problems
- Part of:
-
- Published online by Cambridge University Press:
- 05 March 2025, e51
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Research Article
Rigorous derivation of a binary-ternary Boltzmann equation for a non ideal gas of hard spheres
- Part of:
-
- Published online by Cambridge University Press:
- 05 March 2025, e52
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Discrete Mathematics
Finite Hypergraph Families with Rich Extremal Turán Constructions via Mixing Patterns
- Part of:
-
- Published online by Cambridge University Press:
- 06 March 2025, e53
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Number Theory
Deformations of Theta Integrals and A Conjecture of Gross-Zagier
- Part of:
-
- Published online by Cambridge University Press:
- 14 March 2025, e54
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Discrete Mathematics
Extremal, enumerative and probabilistic results on ordered hypergraph matchings
- Part of:
-
- Published online by Cambridge University Press:
- 14 March 2025, e55
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Topology
Relative quantum cohomology of the Chiang Lagrangian
- Part of:
-
- Published online by Cambridge University Press:
- 17 March 2025, e56
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dynamics
Fiber bundles associated with Anosov representations
- Part of:
-
- Published online by Cambridge University Press:
- 19 March 2025, e57
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Differential Equations
Some remarks on Riesz transforms on exterior Lipschitz domains
- Part of:
-
- Published online by Cambridge University Press:
- 19 March 2025, e58
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Analysis
Nuclearity and
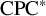 ${\mathrm {CPC}^*}$-Systems
${\mathrm {CPC}^*}$-Systems
- Part of:
-
- Published online by Cambridge University Press:
- 20 March 2025, e59
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebraic and Complex Geometry
k-leaky double Hurwitz descendants
- Part of:
-
- Published online by Cambridge University Press:
- 21 March 2025, e60
-
- Article
-
- You have access
- Open access
- HTML
- Export citation