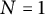 $N=1$ Heisenberg–Virasoro superalgebra
$N=1$ Heisenberg–Virasoro superalgebra
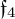 $\mathfrak {f}_4$ AND
$\mathfrak {f}_4$ AND 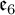 $\mathfrak {e}_6$ VIA CONTACTIFICATIONS
$\mathfrak {e}_6$ VIA CONTACTIFICATIONS
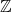 $\mathbb{Z}$-graded identities of the Lie algebras
$\mathbb{Z}$-graded identities of the Lie algebras 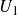 $U_1$ in characteristic 2
$U_1$ in characteristic 2
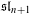 $\mathfrak{sl}_{n+1}$
$\mathfrak{sl}_{n+1}$