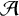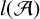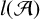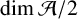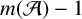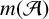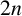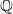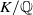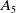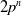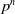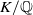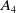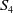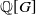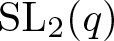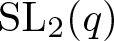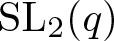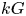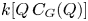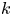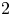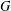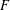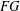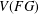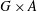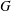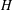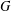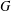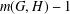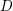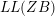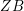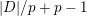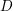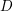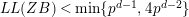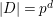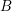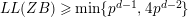Refine search
Actions for selected content:
40 results
AN UPPER BOUND ON THE LENGTH OF AN ALGEBRA AND ITS APPLICATION TO THE GROUP ALGEBRA OF THE DIHEDRAL GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 10 February 2025, pp. 139-148
- Print publication:
- August 2025
-
- Article
- Export citation
Leopoldt-type theorems for non-abelian extensions of
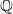 $\mathbb{Q}$
$\mathbb{Q}$
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 22 January 2024, pp. 308-337
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Trivial source character tables of
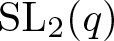 $\operatorname{SL}_2(q)$, part II
$\operatorname{SL}_2(q)$, part II
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 3 / August 2023
- Published online by Cambridge University Press:
- 30 June 2023, pp. 689-709
-
- Article
- Export citation
A Jordan–Hölder theorem for skew left braces and their applications to multipermutation solutions of the Yang–Baxter equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 24 April 2023, pp. 793-809
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Brauer indecomposability of Scott modules with semidihedral vertex
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 04 May 2021, pp. 174-182
-
- Article
- Export citation
A cancellation theorem for modules over integral group rings
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 2 / September 2021
- Published online by Cambridge University Press:
- 27 November 2020, pp. 317-327
- Print publication:
- September 2021
-
- Article
- Export citation
CONNECTIVITY PROPERTIES OF MCKAY QUIVERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 02 October 2020, pp. 182-194
- Print publication:
- April 2021
-
- Article
- Export citation
BLOCKS WITH SMALL-DIMENSIONAL BASIC ALGEBRA
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 21 September 2020, pp. 461-474
- Print publication:
- June 2021
-
- Article
-
- You have access
- Open access
- Export citation
GROUP ALGEBRAS WHOSE UNIT GROUP IS LOCALLY NILPOTENT
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 07 May 2020, pp. 17-23
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
Unitary and Symmetric Units of a Commutative Group Algebra
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 3 / August 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 641-654
-
- Article
- Export citation
Fields of Definition for Representations of Associative Algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 22 November 2018, pp. 291-304
-
- Article
- Export citation
On the First Zassenhaus Conjecture and Direct Products
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 15 October 2018, pp. 602-624
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
OVERGROUPS OF WEAK SECOND MAXIMAL SUBGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 30 August 2018, pp. 83-88
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
WEAK CAYLEY TABLE GROUPS OF SOME CRYSTALLOGRAPHIC GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 28 January 2018, pp. 635-660
- Print publication:
- September 2018
-
- Article
-
- You have access
- Export citation
LOEWY LENGTHS OF CENTERS OF BLOCKS II
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 234 / June 2019
- Published online by Cambridge University Press:
- 25 September 2017, pp. 127-138
- Print publication:
- June 2019
-
- Article
-
- You have access
- HTML
- Export citation
Rational Conjugacy of Torsion Units in Integral Group Rings of Non-Solvable Groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 16 March 2017, pp. 813-830
-
- Article
- Export citation
SOME INFINITE PERMUTATION GROUPS AND RELATED FINITE LINEAR GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 25 October 2016, pp. 136-149
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
THE WORK OF L. G. KOVÁCS ON REPRESENTATION THEORY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 16 June 2015, pp. 34-42
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
The centralizer of a subgroup in a group algebra
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 20 November 2012, pp. 49-56
-
- Article
-
- You have access
- Export citation
On primordial groups for the Green ring
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 24 October 2012, pp. 337-347
-
- Article
-
- You have access
- Export citation