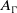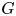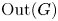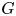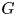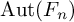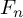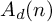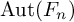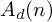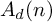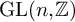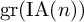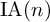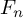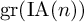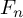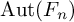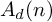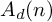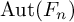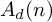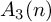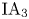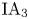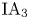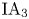Refine search
Actions for selected content:
21 results
A note on morphisms to wreath products
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 08 October 2025, pp. 1-28
-
- Article
- Export citation
On the structures of the Johnson cokernels of the basis-conjugating automorphism groups of free groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 21 July 2025, pp. 1-29
-
- Article
- Export citation
The Formanek-Procesi group with base a right-angled Artin group: Lie algebra and residual nilpotence
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 13 May 2025, pp. 1-22
-
- Article
- Export citation
On automorphisms and splittings of special groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 10 February 2023, pp. 232-305
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ACTIONS OF AUTOMORPHISM GROUPS OF FREE GROUPS ON SPACES OF JACOBI DIAGRAMS. II
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 09 June 2022, pp. 1-69
- Print publication:
- January 2024
-
- Article
- Export citation
On the low-dimensional cohomology groups of the IA-automorphism group of the free group of rank three
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 05 May 2021, pp. 338-363
-
- Article
-
- You have access
- Open access
- Export citation
Cube complexes and abelian subgroups of automorphism groups of RAAGs
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 20 November 2019, pp. 523-547
- Print publication:
- May 2021
-
- Article
- Export citation
CONJUGATING AUTOMORPHISMS OF GRAPH PRODUCTS: KAZHDAN’S PROPERTY (T) AND SQ-UNIVERSALITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 07 August 2019, pp. 272-282
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
Duality between p-groups with three characteristic subgroups and semisimple anti-commutative algebras
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 25 February 2019, pp. 1827-1852
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
WEAK CAYLEY TABLE GROUPS OF SOME CRYSTALLOGRAPHIC GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 28 January 2018, pp. 635-660
- Print publication:
- September 2018
-
- Article
-
- You have access
- Export citation
On the Universal SL2-Representation Rings of Free Groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 30 January 2017, pp. 973-1001
-
- Article
- Export citation
ON THE CENTRE OF THE AUTOMORPHISM GROUP OF A GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 16 June 2015, pp. 390-396
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
Cohomology rings of almost-direct products of free groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 2 / March 2010
- Published online by Cambridge University Press:
- 22 January 2010, pp. 465-479
- Print publication:
- March 2010
-
- Article
-
- You have access
- Export citation
EHRLICH’S THEOREM FOR GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 13 January 2010, pp. 304-309
- Print publication:
- April 2010
-
- Article
-
- You have access
- Export citation
AUTOMORPHISM GROUPS OF THE IMPRIMITIVE COMPLEX REFLECTION GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 86 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 01 February 2009, pp. 123-138
- Print publication:
- February 2009
-
- Article
-
- You have access
- Export citation
AUTOMORPHISM GROUPS OF FREE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 85 / Issue 3 / December 2008
- Published online by Cambridge University Press:
- 01 December 2008, pp. 341-345
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
Some Properties on Isologism of Groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 68 / Issue 1 / February 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-9
- Print publication:
- February 2000
-
- Article
-
- You have access
- Export citation
Semidirect product groups with Abelian automorphism groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 42 / Issue 1 / February 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 84-91
- Print publication:
- February 1987
-
- Article
-
- You have access
- Export citation
2-groups with every automorphism central
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 41 / Issue 2 / October 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 233-236
- Print publication:
- October 1986
-
- Article
-
- You have access
- Export citation
Automorphism orbits of finite groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 40 / Issue 2 / April 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 253-260
- Print publication:
- April 1986
-
- Article
-
- You have access
- Export citation