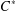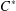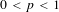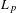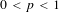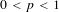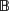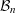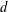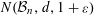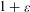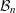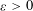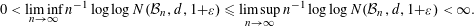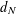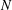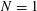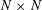Refine search
Actions for selected content:
27 results
Quasi-invariant lifts of completely positive maps for groupoid actions
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 19 August 2025, pp. 1-29
-
- Article
- Export citation
The local geometry of idempotent Schur multipliers
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 March 2025, e14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ANY DUAL OPERATOR SPACE IS WEAKLY LOCALLY REFLEXIVE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 12 December 2023, pp. 158-160
- Print publication:
- August 2024
-
- Article
- Export citation
Which states can be reached from a given state by unital completely positive maps?
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 3 / August 2022
- Published online by Cambridge University Press:
- 05 July 2022, pp. 632-651
-
- Article
- Export citation
Exact structures for operator modules
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 31 January 2022, pp. 421-446
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Weak amenability of free products of hyperbolic and amenable groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 06 January 2022, pp. 698-701
- Print publication:
- September 2022
-
- Article
- Export citation
Amenable dynamical systems over locally compact groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 8 / August 2022
- Published online by Cambridge University Press:
- 25 June 2021, pp. 2468-2508
- Print publication:
- August 2022
-
- Article
- Export citation
NONNEGATIVE POLYNOMIALS, SUMS OF SQUARES AND THE MOMENT PROBLEM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 19 February 2021, pp. 337-341
- Print publication:
- October 2021
-
- Article
-
- You have access
- Export citation
SOME HOMOLOGICAL PROPERTIES OF FOURIER ALGEBRAS ON HOMOGENEOUS SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 09 November 2020, pp. 132-140
- Print publication:
- August 2021
-
- Article
- Export citation
Complete boundedness of multiple operator integrals
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 27 July 2020, pp. 474-490
- Print publication:
- June 2021
-
- Article
- Export citation
APPROXIMATIONS OF SUBHOMOGENEOUS ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 07 February 2019, pp. 328-337
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
A proof of Boca's Theorem
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 869-876
- Print publication:
- August 2019
-
- Article
- Export citation
Andô dilations and inequalities on non-commutative domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 6 / December 2018
- Published online by Cambridge University Press:
- 06 July 2018, pp. 1239-1267
- Print publication:
- December 2018
-
- Article
- Export citation
EMBEDDINGS AND
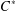 $C^{\ast }$ -ENVELOPES OF EXACT OPERATOR SYSTEMS
$C^{\ast }$ -ENVELOPES OF EXACT OPERATOR SYSTEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 02 May 2017, pp. 274-285
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
Schur Multipliers of Cartan Pairs
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 13 June 2016, pp. 413-440
-
- Article
- Export citation
OPERATOR SYSTEM NUCLEARITY VIA
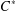 $C^{\ast }$ -ENVELOPES
$C^{\ast }$ -ENVELOPES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 101 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 11 May 2016, pp. 356-375
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
THE NON-COMMUTATIVE KHINTCHINE INEQUALITIES FOR
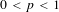 $0<p<1$
$0<p<1$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 16 / Issue 5 / November 2017
- Published online by Cambridge University Press:
- 14 October 2015, pp. 1103-1123
- Print publication:
- November 2017
-
- Article
- Export citation
A CONTINUUM OF C*-NORMS ON
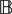 ${\mathbb B}$(H) ⊗
${\mathbb B}$(H) ⊗ 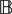 ${\mathbb B}$(H) AND RELATED TENSOR PRODUCTS
${\mathbb B}$(H) AND RELATED TENSOR PRODUCTS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 22 July 2015, pp. 433-443
- Print publication:
- May 2016
-
- Article
-
- You have access
- Export citation
QUOTIENT AND PSEUDO UNIT IN NONUNITAL OPERATOR SYSTEM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 02 April 2015, pp. 123-132
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
ON THE METRIC ENTROPY OF THE BANACH–MAZUR COMPACTUM
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 28 May 2014, pp. 179-198
- Print publication:
- January 2015
-
- Article
- Export citation



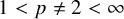

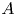
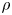
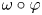
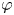
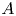
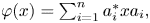
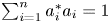
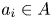
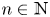
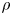
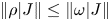
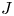
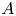
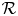
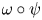
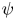
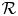
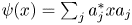
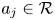
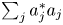
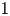

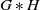
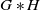
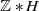
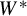
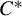
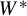
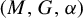
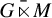
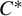
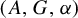
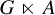
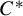
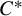

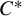
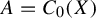
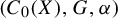
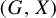
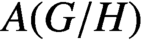
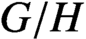
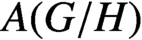
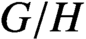
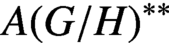
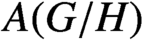

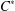



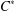
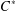
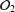
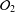
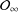
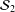
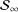
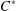
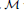 with Cartan maximal abelian self-adjoint algebra
with Cartan maximal abelian self-adjoint algebra  , generalizing the classical Schur multipliers of
, generalizing the classical Schur multipliers of  (
(