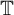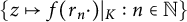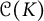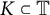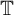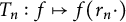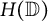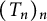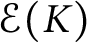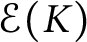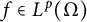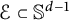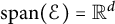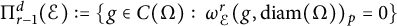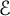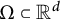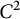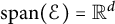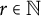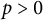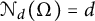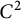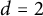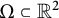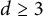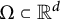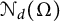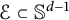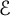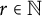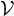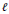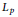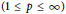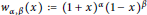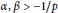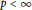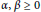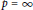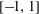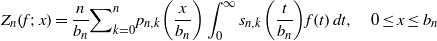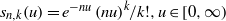Refine search
Actions for selected content:
33 results
Brownian bridge expansions for Lévy area approximations and particular values of the Riemann zeta function
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 03 November 2022, pp. 370-397
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Abel universal functions
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 26 October 2022, pp. 1957-1985
- Print publication:
- December 2023
-
- Article
- Export citation
Quasi-equivalence of bases in some Whitney spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 18 May 2021, pp. 106-115
- Print publication:
- March 2022
-
- Article
- Export citation
On directional Whitney inequality
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 26 February 2021, pp. 833-857
- Print publication:
- June 2022
-
- Article
- Export citation
THE METRIC PROJECTIONS ONTO CLOSED CONVEX CONES IN A HILBERT SPACE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 11 February 2021, pp. 1617-1650
- Print publication:
- September 2022
-
- Article
- Export citation
Optimal approximants and orthogonal polynomials in several variables
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 26 November 2020, pp. 428-456
- Print publication:
- April 2022
-
- Article
-
- You have access
- Open access
- Export citation
APPROXIMATING SMOOTH, MULTIVARIATE FUNCTIONS ON IRREGULAR DOMAINS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 20 May 2020, e26
-
- Article
-
- You have access
- Open access
- Export citation
APPROXIMATION OF AND BY COMPLETELY MONOTONE FUNCTIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 61 / Issue 4 / October 2019
- Published online by Cambridge University Press:
- 06 March 2020, pp. 416-430
-
- Article
-
- You have access
- Export citation
Sparse Recovery via ℓq -Minimization for Polynomial Chaos Expansions
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 10 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 12 September 2017, pp. 775-797
- Print publication:
- November 2017
-
- Article
- Export citation
A Multiple Interval Chebyshev-Gauss-Lobatto Collocation Method for Ordinary Differential Equations
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 9 / Issue 4 / November 2016
- Published online by Cambridge University Press:
- 17 November 2016, pp. 619-639
- Print publication:
- November 2016
-
- Article
- Export citation
Stochastic Collocation via l1-Minimisation on Low Discrepancy Point Sets with Application to Uncertainty Quantification
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 6 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 12 May 2016, pp. 171-191
- Print publication:
- May 2016
-
- Article
- Export citation
Constrained Approximation with Jacobi Weights
-
- Journal:
- Canadian Journal of Mathematics / Volume 68 / Issue 1 / 01 February 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 109-128
- Print publication:
- 01 February 2016
-
- Article
-
- You have access
- Export citation
A note on uniform approximation of functions having a double pole
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 May 2014, pp. 233-244
-
- Article
-
- You have access
- Export citation
Legendre-Gauss Spectral Collocation Method for Second Order Nonlinear Delay Differential Equations
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 7 / Issue 2 / May 2014
- Published online by Cambridge University Press:
- 28 May 2015, pp. 149-178
- Print publication:
- May 2014
-
- Article
- Export citation
Approximation by a composition of Chlodowsky operators and Százs–Durrmeyer operators on weighted spaces
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 01 October 2013, pp. 388-397
-
- Article
-
- You have access
- Export citation
Conforming Hierarchical Basis Functions
-
- Journal:
- Communications in Computational Physics / Volume 12 / Issue 4 / October 2012
- Published online by Cambridge University Press:
- 20 August 2015, pp. 1215-1256
- Print publication:
- October 2012
-
- Article
- Export citation
Some Weighted Averaging Methods for Gradient Recovery
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 4 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 03 June 2015, pp. 131-155
- Print publication:
- April 2012
-
- Article
- Export citation
A Review of David Gottlieb’s Work on the Resolution of the Gibbs Phenomenon
-
- Journal:
- Communications in Computational Physics / Volume 9 / Issue 3 / March 2011
- Published online by Cambridge University Press:
- 20 August 2015, pp. 497-519
- Print publication:
- March 2011
-
- Article
- Export citation
Variance-Based Global Sensitivity Analysis via Sparse-Grid Interpolation and Cubature
-
- Journal:
- Communications in Computational Physics / Volume 9 / Issue 3 / March 2011
- Published online by Cambridge University Press:
- 20 August 2015, pp. 542-567
- Print publication:
- March 2011
-
- Article
- Export citation
Simultaneous Polynomial Approximations of the Lerch Function
-
- Journal:
- Canadian Journal of Mathematics / Volume 61 / Issue 6 / 01 December 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1341-1356
- Print publication:
- 01 December 2009
-
- Article
-
- You have access
- Export citation