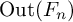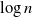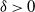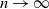Refine search
Actions for selected content:
190 results
The time until a random walk exceeds a square root and other barriers
-
- Journal:
- Probability in the Engineering and Informational Sciences , First View
- Published online by Cambridge University Press:
- 03 September 2025, pp. 1-8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
7 - Random Walkers
-
- Book:
- Probability Theory for Quantitative Scientists
- Published online:
- 24 July 2025
- Print publication:
- 14 August 2025, pp 188-216
-
- Chapter
- Export citation
16 - Transport of Radiation from Interior to Surface
- from Part II - Stellar Structure and Evolution
-
- Book:
- Fundamentals of Astrophysics
- Published online:
- 10 November 2025
- Print publication:
- 24 July 2025, pp 107-111
-
- Chapter
- Export citation
Random walks and contracting elements I: deviation inequality and limit laws
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 17 September 2025, pp. 1512-1575
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
5 - “Fluctuation” of Intracellular Dynamics
-
- Book:
- Theoretical Biology of the Cell
- Published online:
- 05 June 2025
- Print publication:
- 19 June 2025, pp 135-175
-
- Chapter
- Export citation
Infinite-horizon Fuk–Nagaev inequalities
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 16 June 2025, pp. 1076-1088
- Print publication:
- September 2025
-
- Article
- Export citation
2 - Reversible MCMC and Its Scaling
-
- Book:
- Scalable Monte Carlo for Bayesian Learning
- Published online:
- 16 May 2025
- Print publication:
- 05 June 2025, pp 39-61
-
- Chapter
- Export citation
Exact solution to the Chow–Robbins game for almost all n, by using a catalan triangle
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 16 May 2025, pp. 1206-1241
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Chapter 10 - The Timescale of Art History
- from Part II - Entangled Timescales of Visual Arts
-
- Book:
- A Complex Systems View on the Visual Arts
- Published online:
- 20 March 2025
- Print publication:
- 03 April 2025, pp 239-302
-
- Chapter
- Export citation
8 - Random Walks
- from Part II - Pricing by Risk-Neutral Expectation
-
- Book:
- Derivatives Pricing
- Published online:
- 08 July 2025
- Print publication:
- 20 March 2025, pp 199-212
-
- Chapter
- Export citation
First-passage time for Sinai’s random walk in a random environment
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 29 November 2024, pp. 756-774
- Print publication:
- June 2025
-
- Article
- Export citation
3 - Influential Observations
-
- Book:
- Ethics in Econometrics
- Published online:
- 14 November 2024
- Print publication:
- 28 November 2024, pp 54-87
-
- Chapter
- Export citation
7 - Spurious Relations
-
- Book:
- Ethics in Econometrics
- Published online:
- 14 November 2024
- Print publication:
- 28 November 2024, pp 161-185
-
- Chapter
- Export citation
Random walks on groups and superlinear-divergent geodesics
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 21 November 2024, pp. 1403-1443
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
1 - Topics in representation theory of finite groups
-
-
- Book:
- Groups and Graphs, Designs and Dynamics
- Published online:
- 11 May 2024
- Print publication:
- 30 May 2024, pp 1-86
-
- Chapter
- Export citation

Harmonic Functions and Random Walks on Groups
-
- Published online:
- 16 May 2024
- Print publication:
- 23 May 2024
Scaling limit of the local time of random walks conditioned to stay positive
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 13 February 2024, pp. 1060-1074
- Print publication:
- September 2024
-
- Article
- Export citation
Diffusion of H2O in Smectite Gels: Obstruction Effects of Bound H2O Layers
-
- Journal:
- Clays and Clay Minerals / Volume 51 / Issue 1 / February 2003
- Published online by Cambridge University Press:
- 01 January 2024, pp. 9-22
-
- Article
- Export citation
LINEAR GROWTH OF TRANSLATION LENGTHS OF RANDOM ISOMETRIES ON GROMOV HYPERBOLIC SPACES AND TEICHMÜLLER SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 06 November 2023, pp. 1751-1795
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Strong convergence of an epidemic model with mixing groups
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 01 September 2023, pp. 430-463
- Print publication:
- June 2024
-
- Article
- Export citation