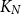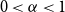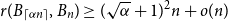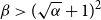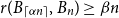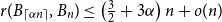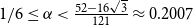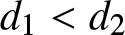Refine search
Actions for selected content:
48580 results in Computer Science
Parameterized complexity of weighted team definability
-
- Journal:
- Mathematical Structures in Computer Science / Volume 34 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 20 February 2024, pp. 375-389
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A content analysis: analyzing topics of conversation under the #sustainability hashtag on Twitter
-
- Journal:
- Environmental Data Science / Volume 3 / 2024
- Published online by Cambridge University Press:
- 20 February 2024, e5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Oscillation-free point-to-point motions of planar differentially flat under-actuated robots: a Laplace transform method
-
- Article
-
- You have access
- Open access
- HTML
- Export citation

Proven Impossible
- Elementary Proofs of Profound Impossibility from Arrow, Bell, Chaitin, Gödel, Turing and More
-
- Published online:
- 18 February 2024
- Print publication:
- 18 January 2024

Topological Duality for Distributive Lattices
- Theory and Applications
-
- Published online:
- 16 February 2024
- Print publication:
- 07 March 2024
On a conjecture of Conlon, Fox, and Wigderson
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 16 February 2024, pp. 432-445
-
- Article
- Export citation
Analyzing the multi-state system under a run shock model
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 4 / October 2024
- Published online by Cambridge University Press:
- 16 February 2024, pp. 619-631
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Explainable and transparent artificial intelligence for public policymaking
-
- Journal:
- Data & Policy / Volume 6 / 2024
- Published online by Cambridge University Press:
- 16 February 2024, e10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Part I - Combinatorial Enumeration
-
- Book:
- Analytic Combinatorics in Several Variables
- Published online:
- 08 February 2024
- Print publication:
- 15 February 2024, pp 1-2
-
- Chapter
- Export citation
3 - Univariate asymptotics
- from Part I - Combinatorial Enumeration
-
- Book:
- Analytic Combinatorics in Several Variables
- Published online:
- 08 February 2024
- Print publication:
- 15 February 2024, pp 60-86
-
- Chapter
- Export citation
Appendix D - Stratification and stratified Morse theory
-
- Book:
- Analytic Combinatorics in Several Variables
- Published online:
- 08 February 2024
- Print publication:
- 15 February 2024, pp 513-532
-
- Chapter
- Export citation
Preface to the second edition
-
- Book:
- Analytic Combinatorics in Several Variables
- Published online:
- 08 February 2024
- Print publication:
- 15 February 2024, pp xi-xiii
-
- Chapter
- Export citation
Appendix B - Algebraic topology
-
- Book:
- Analytic Combinatorics in Several Variables
- Published online:
- 08 February 2024
- Print publication:
- 15 February 2024, pp 462-479
-
- Chapter
- Export citation
Author Index
-
- Book:
- Analytic Combinatorics in Several Variables
- Published online:
- 08 February 2024
- Print publication:
- 15 February 2024, pp 553-558
-
- Chapter
- Export citation
5 - Multivariate Fourier–Laplace integrals
- from Part II - Mathematical Background
-
- Book:
- Analytic Combinatorics in Several Variables
- Published online:
- 08 February 2024
- Print publication:
- 15 February 2024, pp 114-133
-
- Chapter
- Export citation
7 - Overview of analytic methods for multivariate GFs
- from Part III - Multivariate Enumeration
-
- Book:
- Analytic Combinatorics in Several Variables
- Published online:
- 08 February 2024
- Print publication:
- 15 February 2024, pp 169-220
-
- Chapter
- Export citation
List of Symbols
-
- Book:
- Analytic Combinatorics in Several Variables
- Published online:
- 08 February 2024
- Print publication:
- 15 February 2024, pp xvii-xx
-
- Chapter
- Export citation
1 - Introduction
- from Part I - Combinatorial Enumeration
-
- Book:
- Analytic Combinatorics in Several Variables
- Published online:
- 08 February 2024
- Print publication:
- 15 February 2024, pp 3-16
-
- Chapter
- Export citation
Part II - Mathematical Background
-
- Book:
- Analytic Combinatorics in Several Variables
- Published online:
- 08 February 2024
- Print publication:
- 15 February 2024, pp 87-88
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Analytic Combinatorics in Several Variables
- Published online:
- 08 February 2024
- Print publication:
- 15 February 2024, pp i-iv
-
- Chapter
- Export citation