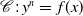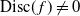Refine search
Actions for selected content:
25839 results in Abstract analysis
Supercritical site percolation on the hypercube: small components are small
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 25 November 2022, pp. 422-427
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Exact nonclassical symmetry solutions of Lotka–Volterra-type population systems
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 25 November 2022, pp. 998-1016
-
- Article
- Export citation

Variations on a Theme of Borel
- An Essay on the Role of the Fundamental Group in Rigidity
-
- Published online:
- 24 November 2022
- Print publication:
- 08 December 2022
Galois representations of superelliptic curves
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 24 November 2022, pp. 356-382
-
- Article
- Export citation
Conjugacy conditions for supersoluble complements of an abelian base and a fixed point result for non-coprime actions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 4 / November 2022
- Published online by Cambridge University Press:
- 24 November 2022, pp. 1075-1079
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
New upper bounds for the Erdős-Gyárfás problem on generalized Ramsey numbers
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 24 November 2022, pp. 349-362
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PRM volume 152 issue 6 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 23 November 2022, pp. b1-b2
- Print publication:
- December 2022
-
- Article
-
- You have access
- Export citation
Double relative commutants in coronas of separable C*-algebras
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 23 November 2022, pp. 345-355
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PRM volume 152 issue 6 Cover and Front matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 23 November 2022, pp. f1-f2
- Print publication:
- December 2022
-
- Article
-
- You have access
- Export citation
Dirichlet vs Neumann
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 4 / November 2022
- Published online by Cambridge University Press:
- 22 November 2022, pp. 1063-1074
-
- Article
- Export citation
Iterates of meromorphic functions on escaping Fatou components
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 22 November 2022, pp. 1906-1928
- Print publication:
- December 2023
-
- Article
- Export citation
Symmetry actions and brackets for adjoint-symmetries. II: Physical examples
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 21 November 2022, pp. 974-997
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Friedrichs extensions for Sturm–Liouville operators with complex coefficients and their spectra
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 18 November 2022, pp. 1883-1905
- Print publication:
- December 2023
-
- Article
- Export citation
Overview
-
- Book:
- Schrödinger Operators: Eigenvalues and Lieb–Thirring Inequalities
- Published online:
- 03 November 2022
- Print publication:
- 17 November 2022, pp 1-4
-
- Chapter
- Export citation
5 - Sharp Lieb–Thirring Inequalities
- from Part Three - Sharp Constants in Lieb–Thirring Inequalities
-
- Book:
- Schrödinger Operators: Eigenvalues and Lieb–Thirring Inequalities
- Published online:
- 03 November 2022
- Print publication:
- 17 November 2022, pp 321-384
-
- Chapter
- Export citation
6 - Sharp Lieb–Thirring Inequalities in Higher Dimensions
- from Part Three - Sharp Constants in Lieb–Thirring Inequalities
-
- Book:
- Schrödinger Operators: Eigenvalues and Lieb–Thirring Inequalities
- Published online:
- 03 November 2022
- Print publication:
- 17 November 2022, pp 385-416
-
- Chapter
- Export citation
Part One - Background Material
-
- Book:
- Schrödinger Operators: Eigenvalues and Lieb–Thirring Inequalities
- Published online:
- 03 November 2022
- Print publication:
- 17 November 2022, pp 5-6
-
- Chapter
- Export citation
Index
-
- Book:
- Schrödinger Operators: Eigenvalues and Lieb–Thirring Inequalities
- Published online:
- 03 November 2022
- Print publication:
- 17 November 2022, pp 504-508
-
- Chapter
- Export citation
Part Two - The Laplace and Schrödinger Operators
-
- Book:
- Schrödinger Operators: Eigenvalues and Lieb–Thirring Inequalities
- Published online:
- 03 November 2022
- Print publication:
- 17 November 2022, pp 165-166
-
- Chapter
- Export citation
References
-
- Book:
- Schrödinger Operators: Eigenvalues and Lieb–Thirring Inequalities
- Published online:
- 03 November 2022
- Print publication:
- 17 November 2022, pp 471-503
-
- Chapter
- Export citation