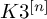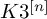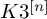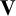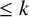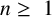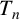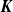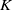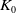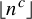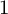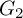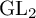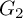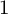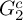Refine search
Actions for selected content:
28975 results in Differential and integral equations, dynamical systems and control theory
JMJ volume 23 issue 1 Cover and Front matter
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 02 February 2024, pp. f1-f2
- Print publication:
- January 2024
-
- Article
-
- You have access
- Export citation
JMJ volume 23 issue 1 Cover and Back matter
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 02 February 2024, pp. b1-b2
- Print publication:
- January 2024
-
- Article
-
- You have access
- Export citation
On a variant of the product replacement algorithm
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 09 January 2024, pp. 221-228
- Print publication:
- January 2024
-
- Article
- Export citation
GMJ volume 66 issue 1 Cover and Back matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 26 February 2024, pp. b1-b2
- Print publication:
- January 2024
-
- Article
-
- You have access
- Export citation
Various topological complexities of small covers and real Bott manifolds
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 27 December 2023, pp. 1061-1086
- Print publication:
- June 2025
-
- Article
- Export citation
RIGID STABLE VECTOR BUNDLES ON HYPERKÄHLER VARIETIES OF TYPE
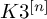 $K3^{[n]}$
$K3^{[n]}$
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 5 / September 2024
- Published online by Cambridge University Press:
- 22 December 2023, pp. 2051-2080
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE PRO-
 $\boldsymbol {k}$-SOLVABLE TOPOLOGY ON A FREE GROUP
$\boldsymbol {k}$-SOLVABLE TOPOLOGY ON A FREE GROUP
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 22 December 2023, pp. 363-383
- Print publication:
- June 2024
-
- Article
- Export citation
The lower bounds of non-real eigenvalues for singular indefinite Sturm–Liouville problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 22 December 2023, pp. 1051-1060
- Print publication:
- June 2025
-
- Article
- Export citation
THE CERESA CLASS: TROPICAL, TOPOLOGICAL AND ALGEBRAIC
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 5 / September 2024
- Published online by Cambridge University Press:
- 21 December 2023, pp. 2175-2215
- Print publication:
- September 2024
-
- Article
- Export citation
Semilinear elliptic equations involving power nonlinearities and Hardy potentials with boundary singularities
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 21 December 2023, pp. 993-1050
- Print publication:
- June 2025
-
- Article
- Export citation
Slices of the Takagi function
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 9 / September 2024
- Published online by Cambridge University Press:
- 20 December 2023, pp. 2361-2398
- Print publication:
- September 2024
-
- Article
- Export citation
QUALITATIVE UNCERTAINTY PRINCIPLE ON CERTAIN LIE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 18 December 2023, pp. 289-307
- Print publication:
- June 2024
-
- Article
- Export citation
NORMAL SUBMONOIDS AND CONGRUENCES ON A MONOID
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 18 December 2023, pp. 331-362
- Print publication:
- June 2024
-
- Article
- Export citation
BRATTELI–VERSHIKISABILITY OF POLYGONAL BILLIARDS ON THE HYPERBOLIC PLANE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 15 December 2023, pp. 85-104
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Levy and Thurston obstructions of finite subdivision rules
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 9 / September 2024
- Published online by Cambridge University Press:
- 15 December 2023, pp. 2649-2699
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Unitary groups,
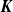 $\boldsymbol{K}$-theory, and traces
$\boldsymbol{K}$-theory, and traces
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 15 December 2023, pp. 229-251
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bracket words along Hardy field sequences
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 9 / September 2024
- Published online by Cambridge University Press:
- 14 December 2023, pp. 2621-2648
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On stable commutator length of non-filling curves in surfaces
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 14 December 2023, pp. 975-992
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Variational inequalities arising from credit rating migration with buffer zone
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 14 December 2023, pp. 515-532
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COUNTING DISCRETE, LEVEL-
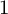 $1$, QUATERNIONIC AUTOMORPHIC REPRESENTATIONS ON
$1$, QUATERNIONIC AUTOMORPHIC REPRESENTATIONS ON 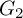 $G_2$
$G_2$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 5 / September 2024
- Published online by Cambridge University Press:
- 13 December 2023, pp. 2127-2157
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation