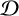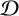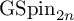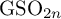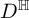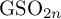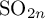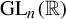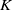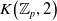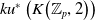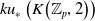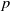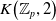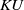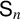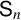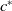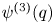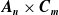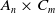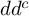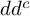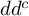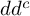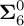Refine search
Actions for selected content:
28975 results in Differential and integral equations, dynamical systems and control theory
FINITELY PRESENTED INVERSE SEMIGROUPS WITH FINITELY MANY IDEMPOTENTS IN EACH
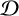 $\mathcal D$-CLASS AND NON-HAUSDORFF UNIVERSAL GROUPOIDS
$\mathcal D$-CLASS AND NON-HAUSDORFF UNIVERSAL GROUPOIDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 13 December 2023, pp. 384-398
- Print publication:
- June 2024
-
- Article
- Export citation
GALOIS REPRESENTATIONS FOR EVEN GENERAL SPECIAL ORTHOGONAL GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 5 / September 2024
- Published online by Cambridge University Press:
- 13 December 2023, pp. 1959-2050
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Invariant measures for substitutions on countable alphabets
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 9 / September 2024
- Published online by Cambridge University Press:
- 11 December 2023, pp. 2533-2564
- Print publication:
- September 2024
-
- Article
- Export citation
A dynamical classification for crossed products of fiberwise essentially minimal zero-dimensional dynamical systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 11 December 2023, pp. 2229-2256
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Equilibrium states for non-uniformly expanding skew products
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 9 / September 2024
- Published online by Cambridge University Press:
- 11 December 2023, pp. 2599-2620
- Print publication:
- September 2024
-
- Article
- Export citation
Random and mean Lyapunov exponents for
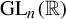 $\operatorname {\mathrm {GL}}_n(\mathbb {R})$
$\operatorname {\mathrm {GL}}_n(\mathbb {R})$
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 11 December 2023, pp. 2063-2079
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The connective
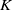 $K$-theory of the Eilenberg–MacLane space
$K$-theory of the Eilenberg–MacLane space 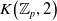 $K\!\left({\mathbb{Z}}_p,\textrm{2}\right)$
$K\!\left({\mathbb{Z}}_p,\textrm{2}\right)$
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 11 December 2023, pp. 188-220
- Print publication:
- January 2024
-
- Article
- Export citation
COMMON ZEROS OF IRREDUCIBLE CHARACTERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 11 December 2023, pp. 105-129
- Print publication:
- October 2024
-
- Article
- Export citation
Analysis and numerical simulations of travelling waves due to plant–soil negative feedback
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 07 December 2023, pp. 554-565
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ETS volume 44 issue 1 Cover and Front matter
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 06 December 2023, pp. f1-f2
- Print publication:
- January 2024
-
- Article
-
- You have access
- Export citation
ETS volume 44 issue 1 Cover and Back matter
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 06 December 2023, pp. b1-b2
- Print publication:
- January 2024
-
- Article
-
- You have access
- Export citation
RODRIGUES FORMULA AND LINEAR INDEPENDENCE FOR VALUES OF HYPERGEOMETRIC FUNCTIONS WITH VARYING PARAMETERS
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 05 December 2023, pp. 308-344
- Print publication:
- December 2024
-
- Article
- Export citation
Propagation dynamics of a mutualistic model of mistletoes and birds with nonlocal dispersal
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 04 December 2023, pp. 533-553
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON LARGE EXTERNALLY DEFINABLE SETS IN NIP
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 5 / September 2024
- Published online by Cambridge University Press:
- 04 December 2023, pp. 2159-2173
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON RESIDUES AND CONJUGACIES FOR GERMS OF 1-D PARABOLIC DIFFEOMORPHISMS IN FINITE REGULARITY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 01 December 2023, pp. 1821-1855
- Print publication:
- July 2024
-
- Article
- Export citation
Partitions with parts separated by parity: conjugation, congruences and the mock theta functions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 30 November 2023, pp. 954-974
- Print publication:
- June 2025
-
- Article
- Export citation
On
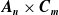 $\boldsymbol{A}_{\boldsymbol{n}} \times \boldsymbol{C}_{\boldsymbol{m}}$-unramified extensions over imaginary quadratic fields
$\boldsymbol{A}_{\boldsymbol{n}} \times \boldsymbol{C}_{\boldsymbol{m}}$-unramified extensions over imaginary quadratic fields
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 29 November 2023, pp. 119-125
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A note on almost Yamabe solitons
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 29 November 2023, pp. 183-187
- Print publication:
- January 2024
-
- Article
- Export citation
A
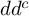 $dd^c$-TYPE CONDITION BEYOND THE KÄHLER REALM
$dd^c$-TYPE CONDITION BEYOND THE KÄHLER REALM
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 28 November 2023, pp. 1651-1704
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
POLISH SPACES OF BANACH SPACES: COMPLEXITY OF ISOMETRY AND ISOMORPHISM CLASSES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 28 November 2023, pp. 1919-1957
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation