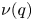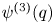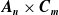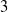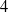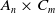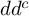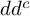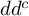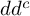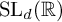Refine search
Actions for selected content:
28981 results in Differential and integral equations, dynamical systems and control theory
ON RESIDUES AND CONJUGACIES FOR GERMS OF 1-D PARABOLIC DIFFEOMORPHISMS IN FINITE REGULARITY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 01 December 2023, pp. 1821-1855
- Print publication:
- July 2024
-
- Article
- Export citation
Partitions with parts separated by parity: conjugation, congruences and the mock theta functions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 30 November 2023, pp. 954-974
- Print publication:
- June 2025
-
- Article
- Export citation
On
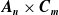 $\boldsymbol{A}_{\boldsymbol{n}} \times \boldsymbol{C}_{\boldsymbol{m}}$-unramified extensions over imaginary quadratic fields
$\boldsymbol{A}_{\boldsymbol{n}} \times \boldsymbol{C}_{\boldsymbol{m}}$-unramified extensions over imaginary quadratic fields
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 29 November 2023, pp. 119-125
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A note on almost Yamabe solitons
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 29 November 2023, pp. 183-187
- Print publication:
- January 2024
-
- Article
- Export citation
A
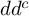 $dd^c$-TYPE CONDITION BEYOND THE KÄHLER REALM
$dd^c$-TYPE CONDITION BEYOND THE KÄHLER REALM
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 28 November 2023, pp. 1651-1704
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
POLISH SPACES OF BANACH SPACES: COMPLEXITY OF ISOMETRY AND ISOMORPHISM CLASSES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 28 November 2023, pp. 1919-1957
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Symmetrized and non-symmetrized asymptotic mean value Laplacian in metric measure spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 28 November 2023, pp. 916-953
- Print publication:
- June 2025
-
- Article
- Export citation
HIGHER MOMENT FORMULAE AND LIMITING DISTRIBUTIONS OF LATTICE POINTS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 5 / September 2024
- Published online by Cambridge University Press:
- 28 November 2023, pp. 2081-2125
- Print publication:
- September 2024
-
- Article
- Export citation
A classification of some thick subcategories in locally noetherian Grothendieck categories
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 23 November 2023, pp. 175-182
- Print publication:
- January 2024
-
- Article
- Export citation
Spaces of functions and sections with paracompact domain
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 21 November 2023, pp. 893-915
- Print publication:
- June 2025
-
- Article
- Export citation
ON GROUPS OF UNITS OF SPECIAL AND ONE-RELATOR INVERSE MONOIDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 21 November 2023, pp. 1875-1918
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
7 - Second Order Differentiability of Convex Functions
- from Part II - Solution of the Monge Problem with Quadratic Cost: The Brenier–McCann Theorem
-
- Book:
- Optimal Mass Transport on Euclidean Spaces
- Published online:
- 02 November 2023
- Print publication:
- 16 November 2023, pp 77-85
-
- Chapter
- Export citation
4 - The Brenier Theorem
- from Part II - Solution of the Monge Problem with Quadratic Cost: The Brenier–McCann Theorem
-
- Book:
- Optimal Mass Transport on Euclidean Spaces
- Published online:
- 02 November 2023
- Print publication:
- 16 November 2023, pp 59-66
-
- Chapter
- Export citation
2 - Discrete Transport Problems
- from Part I - The Kantorovich Problem
-
- Book:
- Optimal Mass Transport on Euclidean Spaces
- Published online:
- 02 November 2023
- Print publication:
- 16 November 2023, pp 14-34
-
- Chapter
- Export citation
Epigraph
-
- Book:
- Optimal Mass Transport on Euclidean Spaces
- Published online:
- 02 November 2023
- Print publication:
- 16 November 2023, pp v-vi
-
- Chapter
- Export citation
Index
-
- Book:
- Optimal Mass Transport on Euclidean Spaces
- Published online:
- 02 November 2023
- Print publication:
- 16 November 2023, pp 294-296
-
- Chapter
- Export citation
14 - The Euler Equations and Isochoric Projections
- from Part III - Applications to PDE and the Calculus of Variations and the Wasserstein Space
-
- Book:
- Optimal Mass Transport on Euclidean Spaces
- Published online:
- 02 November 2023
- Print publication:
- 16 November 2023, pp 164-173
-
- Chapter
- Export citation
15 - Action Minimization, Eulerian Velocities, and Otto's Calculus
- from Part III - Applications to PDE and the Calculus of Variations and the Wasserstein Space
-
- Book:
- Optimal Mass Transport on Euclidean Spaces
- Published online:
- 02 November 2023
- Print publication:
- 16 November 2023, pp 174-192
-
- Chapter
- Export citation
Part III - Applications to PDE and the Calculus of Variations and the Wasserstein Space
-
- Book:
- Optimal Mass Transport on Euclidean Spaces
- Published online:
- 02 November 2023
- Print publication:
- 16 November 2023, pp 95-96
-
- Chapter
- Export citation
5 - First Order Differentiability of Convex Functions
- from Part II - Solution of the Monge Problem with Quadratic Cost: The Brenier–McCann Theorem
-
- Book:
- Optimal Mass Transport on Euclidean Spaces
- Published online:
- 02 November 2023
- Print publication:
- 16 November 2023, pp 67-72
-
- Chapter
- Export citation