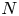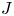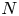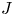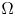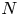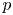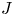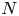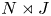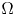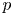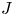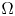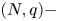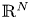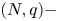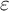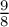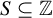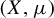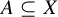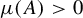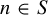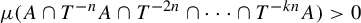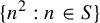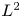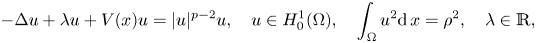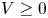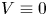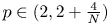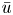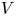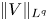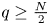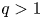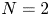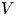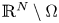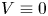Refine search
Actions for selected content:
28888 results in Differential and integral equations, dynamical systems and control theory
Fixed point conditions for non-coprime actions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 11 September 2023, pp. 345-351
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PRM volume 153 issue 5 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 08 September 2023, pp. b1-b2
- Print publication:
- October 2023
-
- Article
-
- You have access
- Export citation
PRM volume 153 issue 5 Cover and Front matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 08 September 2023, pp. f1-f2
- Print publication:
- October 2023
-
- Article
-
- You have access
- Export citation
Stability properties of multidimensional symmetric hyperbolic systems with damping, differential constraints and delay
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 07 September 2023, pp. 199-241
- Print publication:
- February 2025
-
- Article
- Export citation
On the dimension of planar self-affine sets with non-invertible maps
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 07 September 2023, pp. 242-257
- Print publication:
- February 2025
-
- Article
- Export citation
On the linearized Whitham–Broer–Kaup system on bounded domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 07 September 2023, pp. 104-123
- Print publication:
- February 2025
-
- Article
- Export citation
ANZ VOLUME 64 ISSUE 4 COVER AND BACK MATTER
-
- Journal:
- The ANZIAM Journal / Volume 64 / Issue 4 / October 2022
- Published online by Cambridge University Press:
- 07 September 2023, pp. b1-b5
-
- Article
-
- You have access
- Export citation
INDEX
-
- Journal:
- The ANZIAM Journal / Volume 64 / Issue 4 / October 2022
- Published online by Cambridge University Press:
- 07 September 2023, pp. 406-407
-
- Article
- Export citation
Periodic and solitary waves in a Korteweg–de Vries equation with delay
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 07 September 2023, pp. 176-198
- Print publication:
- February 2025
-
- Article
- Export citation
A weighted Trudinger–Moser inequalities and applications to some weighted $(N,q)-$
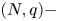 Laplacian equation in $\mathbb {R}^N$
Laplacian equation in $\mathbb {R}^N$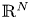 with new exponential growth conditions
with new exponential growth conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 07 September 2023, pp. 124-175
- Print publication:
- February 2025
-
- Article
- Export citation
ANZ VOLUME 64 ISSUE 4 COVER AND FRONT MATTER
-
- Journal:
- The ANZIAM Journal / Volume 64 / Issue 4 / October 2022
- Published online by Cambridge University Press:
- 07 September 2023, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Coupling capacity in C*-algebras
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 07 September 2023, pp. 81-103
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Breakdown of electroneutrality in polyelectrolyte gels
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 06 September 2023, pp. 359-381
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
OPTIMAL GEVREY STABILITY OF HYDROSTATIC APPROXIMATION FOR THE NAVIER-STOKES EQUATIONS IN A THIN DOMAIN
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 06 September 2023, pp. 1521-1566
- Print publication:
- July 2024
-
- Article
- Export citation
ETS volume 43 issue 10 Cover and Front matter
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 10 / October 2023
- Published online by Cambridge University Press:
- 05 September 2023, pp. f1-f2
- Print publication:
- October 2023
-
- Article
-
- You have access
- Export citation
ETS volume 43 issue 10 Cover and Back matter
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 10 / October 2023
- Published online by Cambridge University Press:
- 05 September 2023, pp. b1-b2
- Print publication:
- October 2023
-
- Article
-
- You have access
- Export citation
A set of 2-recurrence whose perfect squares do not form a set of measurable recurrence
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 04 September 2023, pp. 1541-1580
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Discrete heat equation with irregular thermal conductivity and tempered distributional data
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 04 September 2023, pp. 57-80
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Normalized positive solutions for Schrödinger equations with potentials in unbounded domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 04 September 2023, pp. 1518-1551
- Print publication:
- October 2024
-
- Article
- Export citation
Combined effects in mixed local–nonlocal stationary problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 04 September 2023, pp. 10-56
- Print publication:
- February 2025
-
- Article
- Export citation