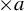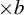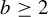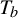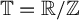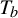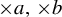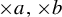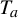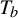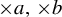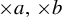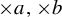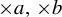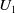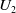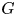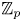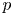Refine search
Actions for selected content:
28888 results in Differential and integral equations, dynamical systems and control theory
Conditional mixing in deterministic chaos
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 18 August 2023, pp. 1693-1723
- Print publication:
- June 2024
-
- Article
- Export citation
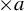 $\times a$ and
$\times a$ and 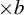 $\times b$ empirical measures, the irregular set and entropy
$\times b$ empirical measures, the irregular set and entropy
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 15 August 2023, pp. 1673-1692
- Print publication:
- June 2024
-
- Article
- Export citation
Toeplitz determinants with a one-cut regular potential and Fisher–Hartwig singularities I. Equilibrium measure supported on the unit circle
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 15 August 2023, pp. 1431-1472
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NUMERICAL SIMULATIONS FOR LARGELY DEFORMED BEAMS AND RINGS ADOPTING A NONTENSILE SMOOTHED PARTICLE HYDRODYNAMICS ALGORITHM
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 64 / Issue 4 / October 2022
- Published online by Cambridge University Press:
- 15 August 2023, pp. 355-379
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Jones polynomial modulo primes
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 15 August 2023, pp. 730-734
- Print publication:
- September 2023
-
- Article
- Export citation
Spreading dynamics of a diffusive epidemic model with free boundaries and two delays
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 11 August 2023, pp. 1133-1169
-
- Article
- Export citation
On classification of singular matrix difference equations of mixed order
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 11 August 2023, pp. 1235-1258
- Print publication:
- August 2024
-
- Article
- Export citation
On the structure of lower bounded HNN extensions
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 10 August 2023, pp. 697-715
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BURSTING SOLUTIONS OF THE RÖSSLER EQUATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 65 / Issue 1-2 / January 2023
- Published online by Cambridge University Press:
- 10 August 2023, pp. 93-110
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JMJ volume 22 issue 5 Cover and Back matter
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 09 August 2023, pp. b1-b2
- Print publication:
- September 2023
-
- Article
-
- You have access
- Export citation
JMJ volume 22 issue 5 Cover and Front matter
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 09 August 2023, pp. f1-f2
- Print publication:
- September 2023
-
- Article
-
- You have access
- Export citation
ETS volume 43 issue 9 Cover and Back matter
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 9 / September 2023
- Published online by Cambridge University Press:
- 08 August 2023, pp. b1-b2
- Print publication:
- September 2023
-
- Article
-
- You have access
- Export citation
Characterising small objects in the regime between the eddy current model and wave propagation
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 08 August 2023, pp. 294-317
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The effect of pore-scale contaminant distribution on the reactive decontamination of porous media
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 08 August 2023, pp. 318-358
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ETS volume 43 issue 9 Cover and Front matter
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 9 / September 2023
- Published online by Cambridge University Press:
- 08 August 2023, pp. f1-f2
- Print publication:
- September 2023
-
- Article
-
- You have access
- Export citation
Sharp constants in inequalities admitting the Calderón transference principle
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 04 August 2023, pp. 1597-1608
- Print publication:
- June 2024
-
- Article
- Export citation
On the dimension of stationary measures for random piecewise affine interval homeomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 04 August 2023, pp. 1473-1488
- Print publication:
- June 2024
-
- Article
- Export citation
Reflexive homology
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 03 August 2023, pp. 1378-1405
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Encoding subshifts through sliding block codes
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 03 August 2023, pp. 1609-1628
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Fixed point sets and the fundamental group I: semi-free actions on G-CW-complexes
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 03 August 2023, pp. 1639-1660
- Print publication:
- December 2024
-
- Article
- Export citation