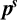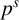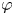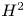Refine search
Actions for selected content:
28894 results in Differential and integral equations, dynamical systems and control theory
ETS volume 43 issue 9 Cover and Front matter
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 9 / September 2023
- Published online by Cambridge University Press:
- 08 August 2023, pp. f1-f2
- Print publication:
- September 2023
-
- Article
-
- You have access
- Export citation
Sharp constants in inequalities admitting the Calderón transference principle
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 04 August 2023, pp. 1597-1608
- Print publication:
- June 2024
-
- Article
- Export citation
On the dimension of stationary measures for random piecewise affine interval homeomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 04 August 2023, pp. 1473-1488
- Print publication:
- June 2024
-
- Article
- Export citation
Reflexive homology
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 03 August 2023, pp. 1378-1405
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Encoding subshifts through sliding block codes
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 03 August 2023, pp. 1609-1628
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Fixed point sets and the fundamental group I: semi-free actions on G-CW-complexes
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 03 August 2023, pp. 1639-1660
- Print publication:
- December 2024
-
- Article
- Export citation
GHOSTS AND CONGRUENCES FOR
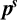 $\boldsymbol {p}^{\boldsymbol {s}}$-APPROXIMATIONS OF HYPERGEOMETRIC PERIODS
$\boldsymbol {p}^{\boldsymbol {s}}$-APPROXIMATIONS OF HYPERGEOMETRIC PERIODS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 02 August 2023, pp. 96-127
- Print publication:
- February 2024
-
- Article
- Export citation
THE ROLE OF THE MATHEMATICAL SCIENCES IN SUPPORTING THE COVID-19 RESPONSE IN AUSTRALIA AND NEW ZEALAND
-
- Journal:
- The ANZIAM Journal / Volume 64 / Issue 4 / October 2022
- Published online by Cambridge University Press:
- 31 July 2023, pp. 315-337
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Poincaré complex diagonals and the Bass trace conjecture
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 28 July 2023, pp. 1819-1840
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Finite domination and Novikov homology over strongly $\mathbb {Z}^2$
 -graded rings
-graded rings
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 28 July 2023, pp. 1786-1818
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Avoidance loci and tropicalizations of real bitangents to plane quartics
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 26 July 2023, pp. 1308-1312
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A symmetry of silting quivers
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 26 July 2023, pp. 687-696
- Print publication:
- September 2023
-
- Article
- Export citation
A presentation for the Eisenstein-Picard modular group in three complex dimensions
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 25 July 2023, pp. 625-654
- Print publication:
- September 2023
-
- Article
- Export citation
Geometric aspects on Humbert-Edge curves of type 5, Kummer surfaces and hyperelliptic curves of genus 2
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 25 July 2023, pp. 612-624
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
HALL CLASSES OF GROUPS WITH A LOCALLY FINITE OBSTRUCTION
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 24 July 2023, pp. 16-43
- Print publication:
- August 2024
-
- Article
- Export citation
Orbits closeness for slowly mixing dynamical systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 24 July 2023, pp. 1192-1208
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Schatten class composition operators on the Hardy space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 24 July 2023, pp. 1364-1377
- Print publication:
- October 2024
-
- Article
- Export citation
AN EXAMINATION OF THE “LANIER WING” DESIGN
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 65 / Issue 1-2 / January 2023
- Published online by Cambridge University Press:
- 21 July 2023, pp. 155-177
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Appendix J - Open problems
-
- Book:
- Lectures on Lagrangian Torus Fibrations
- Published online:
- 06 July 2023
- Print publication:
- 20 July 2023, pp 207-212
-
- Chapter
- Export citation
8 - Almost toric manifolds
-
- Book:
- Lectures on Lagrangian Torus Fibrations
- Published online:
- 06 July 2023
- Print publication:
- 20 July 2023, pp 100-121
-
- Chapter
- Export citation