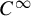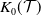Refine search
Actions for selected content:
28895 results in Differential and integral equations, dynamical systems and control theory
On the abundance of k-fold semi-monotone minimal sets in bimodal circle maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 12 July 2023, pp. 1269-1314
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On large solutions for fractional Hamilton–Jacobi equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 11 July 2023, pp. 1313-1335
- Print publication:
- October 2024
-
- Article
- Export citation
On infinitely many foliations by caustics in strictly convex open billiards
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 11 July 2023, pp. 1418-1467
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dynamics and steady state of squirmer motion in liquid crystal
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 10 July 2023, pp. 225-266
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generalized tilting theory in functor categories
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 10 July 2023, pp. 595-611
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ETS volume 43 issue 8 Cover and Back matter
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 8 / August 2023
- Published online by Cambridge University Press:
- 07 July 2023, pp. b1-b2
- Print publication:
- August 2023
-
- Article
-
- You have access
- Export citation
ETS volume 43 issue 8 Cover and Front matter
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 8 / August 2023
- Published online by Cambridge University Press:
- 07 July 2023, pp. f1-f2
- Print publication:
- August 2023
-
- Article
-
- You have access
- Export citation
Instability of axisymmetric flow in thermocapillary liquid bridges: Kinetic and thermal energy budgets for two-phase flow with temperature-dependent material properties
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 07 July 2023, pp. 267-293
-
- Article
-
- You have access
- Open access
- HTML
- Export citation

Lectures on Lagrangian Torus Fibrations
-
- Published online:
- 06 July 2023
- Print publication:
- 20 July 2023
Resilience of dynamical systems – ERRATUM
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 06 July 2023, p. 201
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PRM volume 153 issue 4 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 06 July 2023, pp. b1-b2
- Print publication:
- August 2023
-
- Article
-
- You have access
- Export citation
Subrepresentations in the homology of finite covers of graphs
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 06 July 2023, pp. 582-594
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PRM volume 153 issue 4 Cover and Front matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 06 July 2023, pp. f1-f2
- Print publication:
- August 2023
-
- Article
-
- You have access
- Export citation
Finitely presented left orderable monsters
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 06 July 2023, pp. 1367-1378
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Word complexity of (measure-theoretically) weakly mixing rank-one subshifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 05 July 2023, pp. 1330-1366
- Print publication:
- May 2024
-
- Article
- Export citation
MORAVA K-THEORY AND FILTRATIONS BY POWERS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 5 / September 2025
- Published online by Cambridge University Press:
- 04 July 2023, pp. 1655-1731
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MODELLING MICROWAVES IN BAUXITE
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 65 / Issue 1-2 / January 2023
- Published online by Cambridge University Press:
- 04 July 2023, pp. 111-134
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JMJ volume 22 issue 4 Cover and Front matter
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 06 July 2023, pp. f1-f2
- Print publication:
- July 2023
-
- Article
-
- You have access
- Export citation
JMJ volume 22 issue 4 Cover and Back matter
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 06 July 2023, pp. b1-b2
- Print publication:
- July 2023
-
- Article
-
- You have access
- Export citation
Deformations of corank 1 frontals
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 26 June 2023, pp. 1204-1234
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation