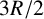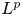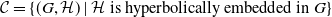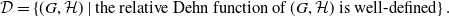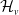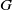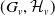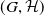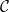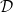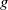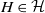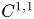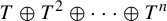Refine search
Actions for selected content:
28888 results in Differential and integral equations, dynamical systems and control theory
Mutating signed
 $\tau$-exceptional sequences
$\tau$-exceptional sequences
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 12 October 2023, pp. 716-729
- Print publication:
- September 2023
-
- Article
- Export citation
GMJ volume 65 issue 3 Cover and Back matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 12 October 2023, pp. b1-b2
- Print publication:
- September 2023
-
- Article
-
- You have access
- Export citation
GMJ volume 65 issue 3 Cover and Front matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 12 October 2023, pp. f1-f2
- Print publication:
- September 2023
-
- Article
-
- You have access
- Export citation
Quantum symmetries of Cayley graphs of abelian groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 12 October 2023, pp. 655-686
- Print publication:
- September 2023
-
- Article
- Export citation
A spectral refinement of the Bergelson–Host–Kra decomposition and new multiple ergodic theorems – CORRIGENDUM
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 01 September 2023, pp. 1724-1728
- Print publication:
- June 2024
-
- Article
-
- You have access
- HTML
- Export citation
WALL STABILIZATION IN MINES BY SPRAY-ON LINERS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 65 / Issue 1-2 / January 2023
- Published online by Cambridge University Press:
- 31 August 2023, pp. 55-78
-
- Article
- Export citation
NUMERICAL ANALYSIS OF APPARATUS-INDUCED DISPERSION FOR DENSITY-DEPENDENT SOLUTE TRANSPORT IN POROUS MEDIA
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 65 / Issue 1-2 / January 2023
- Published online by Cambridge University Press:
- 31 August 2023, pp. 178-194
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Nonchaotic N-expansive homeomorphisms
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 31 August 2023, pp. 1-9
- Print publication:
- February 2025
-
- Article
- Export citation
A nonconservative kinetic framework under the action of an external force field: Theoretical results with application inspired to ecology
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 31 August 2023, pp. 1170-1186
-
- Article
- Export citation
Sharp Sobolev regularity of restricted X-ray transforms
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 30 August 2023, pp. 1583-1603
- Print publication:
- October 2024
-
- Article
- Export citation
Rotating periodic solutions for p-Laplacian differential systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 30 August 2023, pp. 1604-1633
- Print publication:
- October 2024
-
- Article
- Export citation
Moser's theorem with frequency-preserving
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 29 August 2023, pp. 1473-1503
- Print publication:
- October 2024
-
- Article
- Export citation
Relative Dehn functions, hyperbolically embedded subgroups and combination theorems
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 25 August 2023, pp. 1-23
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Synthetic versus distributional lower Ricci curvature bounds
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 23 August 2023, pp. 1406-1430
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ODD RANK VECTOR BUNDLES IN ETA-PERIODIC MOTIVIC HOMOTOPY THEORY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 23 August 2023, pp. 1-32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AN IMEX-BASED APPROACH FOR THE PRICING OF EQUITY WARRANTS UNDER FRACTIONAL BROWNIAN MOTION MODELS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 64 / Issue 4 / October 2022
- Published online by Cambridge University Press:
- 23 August 2023, pp. 380-393
-
- Article
- Export citation
NOVEL STABILITY CONDITIONS FOR SOME GENERALIZATION OF NICHOLSON’S BLOWFLIES MODEL WITH STOCHASTIC PERTURBATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 64 / Issue 4 / October 2022
- Published online by Cambridge University Press:
- 23 August 2023, pp. 394-405
-
- Article
- Export citation
Remarks on countable subadditivity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 23 August 2023, pp. 1504-1517
- Print publication:
- October 2024
-
- Article
- Export citation
Disjoint hypercyclicity, Sidon sets and weakly mixing operators
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 22 August 2023, pp. 1315-1329
- Print publication:
- May 2024
-
- Article
- Export citation
Tame or wild Toeplitz shifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 18 August 2023, pp. 1379-1417
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation