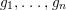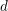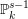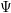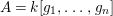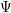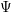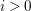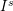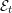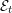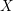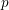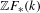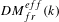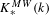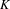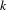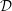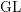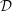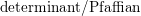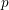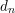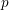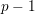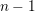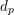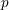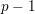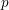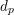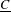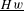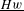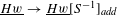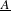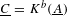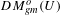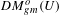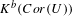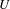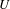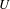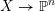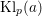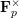Refine listing
Actions for selected content:
378 results in 14Fxx
On log del Pezzo surfaces in large characteristic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 4 / April 2017
- Published online by Cambridge University Press:
- 08 March 2017, pp. 820-850
- Print publication:
- April 2017
-
- Article
- Export citation
The K3 category of a cubic fourfold
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 3 / March 2017
- Published online by Cambridge University Press:
- 02 March 2017, pp. 586-620
- Print publication:
- March 2017
-
- Article
-
- You have access
- HTML
- Export citation
Divisorial Models of Normal Varieties
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 31 January 2017, pp. 1053-1064
-
- Article
- Export citation
Differential Graded Quivers of Smooth Rational Surfaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 15 December 2016, pp. 859-876
-
- Article
- Export citation
The affine Grassmannian and the Springer resolution in positive characteristic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 12 / December 2016
- Published online by Cambridge University Press:
- 28 November 2016, pp. 2627-2677
- Print publication:
- December 2016
-
- Article
- Export citation
Supernatural analogues of Beilinson monads
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 12 / December 2016
- Published online by Cambridge University Press:
- 14 November 2016, pp. 2545-2562
- Print publication:
- December 2016
-
- Article
- Export citation
An approach to intersection theory on singular varieties using motivic complexes
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 11 / November 2016
- Published online by Cambridge University Press:
- 08 November 2016, pp. 2371-2404
- Print publication:
- November 2016
-
- Article
- Export citation
A RECOLLEMENT APPROACH TO GEIGLE–LENZING WEIGHTED PROJECTIVE VARIETIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 226 / June 2017
- Published online by Cambridge University Press:
- 13 October 2016, pp. 71-105
- Print publication:
- June 2017
-
- Article
-
- You have access
- HTML
- Export citation
SKETCHES IN HIGHER CATEGORY THEORY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 26 September 2016, p. 164
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
BLOWUPS AND FIBERS OF MORPHISMS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 224 / Issue 1 / December 2016
- Published online by Cambridge University Press:
- 13 September 2016, pp. 168-201
- Print publication:
- December 2016
-
- Article
-
- You have access
- HTML
- Export citation
A boundedness theorem for nearby slopes of holonomic
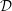 ${\mathcal{D}}$ -modules
${\mathcal{D}}$ -modules
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 10 / October 2016
- Published online by Cambridge University Press:
- 09 September 2016, pp. 2050-2070
- Print publication:
- October 2016
-
- Article
- Export citation
Reciprocity sheaves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 9 / September 2016
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1851-1898
- Print publication:
- September 2016
-
- Article
- Export citation
A higher-dimensional generalization of Lichtenbaum duality in terms of the Albanese map
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 9 / September 2016
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1915-1934
- Print publication:
- September 2016
-
- Article
- Export citation
FRAMED CORRESPONDENCES AND THE MILNOR–WITT
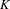 $K$-THEORY
$K$-THEORY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 4 / September 2018
- Published online by Cambridge University Press:
- 30 June 2016, pp. 823-852
- Print publication:
- September 2018
-
- Article
- Export citation
Characters of equivariant
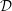 ${\mathcal{D}}$ -modules on spaces of matrices
${\mathcal{D}}$ -modules on spaces of matrices
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 9 / September 2016
- Published online by Cambridge University Press:
- 28 June 2016, pp. 1935-1965
- Print publication:
- September 2016
-
- Article
- Export citation
Motivic cohomology spectral sequence and Steenrod operations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 10 / October 2016
- Published online by Cambridge University Press:
- 24 June 2016, pp. 2113-2133
- Print publication:
- October 2016
-
- Article
- Export citation
NON-COMMUTATIVE LOCALIZATIONS OF ADDITIVE CATEGORIES AND WEIGHT STRUCTURES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 4 / September 2018
- Published online by Cambridge University Press:
- 24 May 2016, pp. 785-821
- Print publication:
- September 2018
-
- Article
- Export citation
Grothendieck–Neeman duality and the Wirthmüller isomorphism
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 8 / August 2016
- Published online by Cambridge University Press:
- 23 May 2016, pp. 1740-1776
- Print publication:
- August 2016
-
- Article
- Export citation
Failures of weak approximation in families
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 7 / July 2016
- Published online by Cambridge University Press:
- 26 April 2016, pp. 1435-1475
- Print publication:
- July 2016
-
- Article
- Export citation
Kloosterman paths and the shape of exponential sums
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 7 / July 2016
- Published online by Cambridge University Press:
- 15 April 2016, pp. 1489-1516
- Print publication:
- July 2016
-
- Article
- Export citation
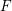
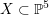
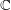
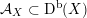
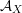
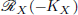 is finitely generated. We introduce a notion of nefness for non-ℚ-Gorenstein varieties and study some of its properties. We then focus on these properties for non-ℚ-Gorenstein toric varieties.
is finitely generated. We introduce a notion of nefness for non-ℚ-Gorenstein varieties and study some of its properties. We then focus on these properties for non-ℚ-Gorenstein toric varieties.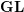
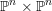
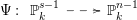 defined by homogeneous forms
defined by homogeneous forms