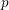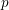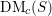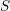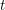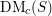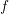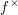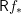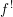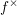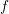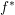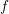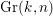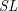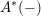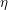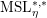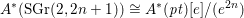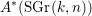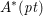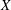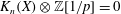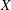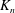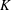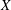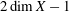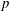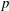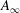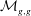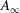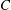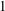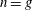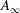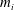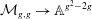Refine listing
Actions for selected content:
378 results in 14Fxx
Computing Néron–Severi groups and cycle class groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 4 / April 2015
- Published online by Cambridge University Press:
- 04 February 2015, pp. 713-734
- Print publication:
- April 2015
-
- Article
- Export citation
Mixed motivic sheaves (and weights for them) exist if ‘ordinary’ mixed motives do
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 5 / May 2015
- Published online by Cambridge University Press:
- 09 January 2015, pp. 917-956
- Print publication:
- May 2015
-
- Article
- Export citation
ADHM CONSTRUCTION OF PERVERSE INSTANTON SHEAVES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 2 / May 2015
- Published online by Cambridge University Press:
- 18 December 2014, pp. 285-321
- Print publication:
- May 2015
-
- Article
-
- You have access
- Export citation
THE DERIVED CATEGORY OF AN ÉTALE EXTENSION AND THE SEPARABLE NEEMAN–THOMASON THEOREM
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 3 / July 2016
- Published online by Cambridge University Press:
- 12 December 2014, pp. 613-623
- Print publication:
- July 2016
-
- Article
-
- You have access
- Export citation
Représentations linéaires des groupes kählériens : factorisations et conjecture de Shafarevich linéaire
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 2 / February 2015
- Published online by Cambridge University Press:
- 26 November 2014, pp. 351-376
- Print publication:
- February 2015
-
- Article
- Export citation
Relation between two twisted inverse image pseudofunctors in duality theory
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 4 / April 2015
- Published online by Cambridge University Press:
- 19 November 2014, pp. 735-764
- Print publication:
- April 2015
-
- Article
- Export citation
The special linear version of the projective bundle theorem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 3 / March 2015
- Published online by Cambridge University Press:
- 07 November 2014, pp. 461-501
- Print publication:
- March 2015
-
- Article
- Export citation
DERIVED ALGEBRAIC COBORDISM
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 30 October 2014, pp. 407-443
- Print publication:
- April 2016
-
- Article
- Export citation
Numerical dimension and a Kawamata–Viehweg–Nadel-type vanishing theorem on compact Kähler manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 11 / November 2014
- Published online by Cambridge University Press:
- 27 August 2014, pp. 1869-1902
- Print publication:
- November 2014
-
- Article
- Export citation
KAROUBI’S RELATIVE CHERN CHARACTER, THE RIGID SYNTOMIC REGULATOR, AND THE BLOCH–KATO EXPONENTIAL MAP
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 2 / 01 July 2014
- Published online by Cambridge University Press:
- 20 August 2014, e20
-
- Article
-
- You have access
- Open access
- Export citation
Vanishing of negative
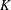 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}K$-theory in positive characteristic
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}K$-theory in positive characteristic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 8 / August 2014
- Published online by Cambridge University Press:
- 17 July 2014, pp. 1425-1434
- Print publication:
- August 2014
-
- Article
- Export citation
Characterization of products of theta divisors
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 8 / August 2014
- Published online by Cambridge University Press:
- 30 June 2014, pp. 1384-1412
- Print publication:
- August 2014
-
- Article
- Export citation
Fourier–Mukai functors in the supported case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 8 / August 2014
- Published online by Cambridge University Press:
- 30 June 2014, pp. 1349-1383
- Print publication:
- August 2014
-
- Article
- Export citation
CHOW GROUPS, CHOW COHOMOLOGY, AND LINEAR VARIETIES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 2 / 01 July 2014
- Published online by Cambridge University Press:
- 24 June 2014, e17
-
- Article
-
- You have access
- Open access
- Export citation
THE RIGID SYNTOMIC RING SPECTRUM
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 14 / Issue 4 / October 2015
- Published online by Cambridge University Press:
- 13 June 2014, pp. 753-799
- Print publication:
- October 2015
-
- Article
- Export citation
ON THE FORMAL AFFINE HECKE ALGEBRA
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 14 / Issue 4 / October 2015
- Published online by Cambridge University Press:
- 09 June 2014, pp. 837-855
- Print publication:
- October 2015
-
- Article
- Export citation
An injectivity theorem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 6 / June 2014
- Published online by Cambridge University Press:
- 12 May 2014, pp. 999-1023
- Print publication:
- June 2014
-
- Article
- Export citation
Product formula for p -adic epsilon factors
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 14 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 08 May 2014, pp. 275-377
- Print publication:
- April 2015
-
- Article
- Export citation
Window shifts, flop equivalences and Grassmannian twists
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 6 / June 2014
- Published online by Cambridge University Press:
- 07 April 2014, pp. 942-978
- Print publication:
- June 2014
-
- Article
- Export citation
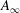 $A_{\infty }$-algebras associated with curves and rational functions on
$A_{\infty }$-algebras associated with curves and rational functions on 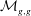 $\mathcal{M}_{g,g}$. I
$\mathcal{M}_{g,g}$. I
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 4 / April 2014
- Published online by Cambridge University Press:
- 10 March 2014, pp. 621-667
- Print publication:
- April 2014
-
- Article
- Export citation