The main goal of this paper is to deduce (from a recent resolution of singularities result of Gabber) the following fact: (effective) Chow motives with ℤ[1/p]-coefficients over a perfect field k of characteristic p generate the category DMeffgm[1/p] (of effective geometric Voevodsky’s motives with ℤ[1/p]-coefficients). It follows that DMeffgm[1/p] can be endowed with a Chow weight structure wChow whose heart is Choweff[1/p] (weight structures were introduced in a preceding paper, where the existence of wChow for DMeffgmℚ was also proved). As shown in previous papers, this statement immediately yields the existence of a conservative weight complex functor DMeffgm[1/p]→Kb (Choweff [1/p])(which induces an isomorphism on K0-groups), as well as the existence of canonical and functorial (Chow)-weight spectral sequences and weight filtrations for any cohomology theory on DMeffgm[1/p] . We also mention a certain Chow t-structure for DMeff−[1/p]and relate it with unramified cohomology.

In this article we consider exceptional sequences of invertible sheaves on smooth complete rational surfaces. We show that to every such sequence one can associate a smooth complete toric surface in a canonical way. We use this structural result to prove various theorems on exceptional and strongly exceptional sequences of invertible sheaves on rational surfaces. We construct full strongly exceptional sequences for a large class of rational surfaces. For the case of toric surfaces we give a complete classification of full strongly exceptional sequences of invertible sheaves.

We complete our proof that given an overconvergent F-isocrystal on a variety over a field of positive characteristic, one can pull back along a suitable generically finite cover to obtain an isocrystal which extends, with logarithmic singularities and nilpotent residues, to some complete variety. We also establish an analogue for F-isocrystals overconvergent inside a partial compactification. By previous results, this reduces to solving a local problem in a neighborhood of a valuation of height 1 and residual transcendence degree zero. We do this by studying the variation of some numerical invariants attached to p-adic differential modules, analogous to the irregularity of a complex meromorphic connection. This allows for an induction on the transcendence defect of the valuation, i.e., the discrepancy between the dimension of the variety and the rational rank of the valuation.

Let k be a field of characteristic zero, let G be a connected reductive algebraic group over k and let 𝔤 be its Lie algebra. Let k(G), respectively, k(𝔤), be the field of k-rational functions on G, respectively, 𝔤. The conjugation action of G on itself induces the adjoint action of G on 𝔤. We investigate the question whether or not the field extensions k(G)/k(G)G and k(𝔤)/k(𝔤)G are purely transcendental. We show that the answer is the same for k(G)/k(G)G and k(𝔤)/k(𝔤)G, and reduce the problem to the case where G is simple. For simple groups we show that the answer is positive if G is split of type An or Cn, and negative for groups of other types, except possibly G2. A key ingredient in the proof of the negative result is a recent formula for the unramified Brauer group of a homogeneous space with connected stabilizers. As a byproduct of our investigation we give an affirmative answer to a question of Grothendieck about the existence of a rational section of the categorical quotient morphism for the conjugating action of G on itself.

Laumon introduced the local Fourier transform for ℓ-adic Galois representations of local fields, of equal characteristic p different from ℓ, as a powerful tool for studying the Fourier–Deligne transform of ℓ-adic sheaves over the affine line. In this article, we compute explicitly the local Fourier transform of monomial representations satisfying a certain ramification condition, and deduce Laumon’s formula relating the ε-factor to the determinant of the local Fourier transform under the same condition.

This paper studies affine Deligne–Lusztig varieties in the affine flag manifold of a split group. Among other things, it proves emptiness for certain of these varieties, relates some of them to those for Levi subgroups, and extends previous conjectures concerning their dimensions. We generalize the superset method, an algorithmic approach to the questions of non-emptiness and dimension. Our non-emptiness results apply equally well to the p-adic context and therefore relate to moduli of p-divisible groups and Shimura varieties with Iwahori level structure.

Let K be a complete discrete valuation field of mixed characteristic (0,p) with a perfect residue field k. For a semi-stable scheme over the ring of integers OK of K or, more generally, for a log smooth scheme of semi-stable type over k, we define nearby cycles as a single 𝒟-module endowed with a monodromy ∂logt, whose cohomology should give the log crystalline cohomology. We also explicitly describe the monodromy filtration of the 𝒟-module with respect to the endomorphism ∂logt, and construct a weight spectral sequence for the cohomology of the nearby cycles.

Using a local construction from a previous paper, we exhibit a numerical invariant, the differential Swan conductor, for an isocrystal on a variety over a perfect field of positive characteristic overconvergent along a boundary divisor; this leads to an analogous construction for certain p-adic and l-adic representations of the étale fundamental group of a variety. We then demonstrate some variational properties of this definition for overconvergent isocrystals, paying special attention to the case of surfaces.

Katz’s middle convolution algorithm provides a description of rigid connections on ℙ1 with regular singularities. We extend the algorithm by adding the Fourier transform to it. The extended algorithm provides a description of rigid connections with arbitrary singularities.

Using the middle convolution functor MCχ introduced by N. Katz, we prove the existence of rigid local systems whose monodromy is dense in the simple algebraic group G2. We derive the existence of motives for motivated cycles which have a motivic Galois group of type G2. Granting Grothendieck’s standard conjectures, the existence of motives with motivic Galois group of type G2 can be deduced, giving a partial answer to a question of Serre.

In this paper, we define Swan conductors for unit-root overconvergent F-isocrystals using the theory of arithmetic 𝒟-modules due to Berthelot. Our Swan conductors are compared with the Swan conductors for ℓ-adic sheaves constructed by Kato and Saito using a geometric method. As an application, we prove the integrality of Swan conductors in the sense of Kato and Saito under the ‘resolution of singularities’ assumption.

Let X be a smooth projective variety defined over an algebraically closed field k. Nori constructed a category of vector bundles on X, called essentially finite vector bundles, which is reminiscent of the category of representations of the fundamental group (in characteristic zero). In fact, this category is equivalent to the category of representations of a pro-finite group scheme which controls all finite torsors. We show that essentially finite vector bundles coincide with those which become trivial after being pulled back by some proper and surjective morphism to X.

We show that the limit of a one-parameter admissible normal function with no singularities lies in a non-classical sub-object of the limiting intermediate Jacobian. Using this, we construct a Hausdorff slit analytic space, with complex Lie group fibres, which ‘graphs’ such normal functions. For singular normal functions, an extension of the sub-object by a finite group leads to the Néron models. When the normal function comes from geometry, that is, a family of algebraic cycles on a semistably degenerating family of varieties, its limit may be interpreted via the Abel–Jacobi map on motivic cohomology of the singular fibre, hence via regulators on K-groups of its substrata. Two examples are worked out in detail, for families of 1-cycles on CY and abelian 3-folds, where this produces interesting arithmetic constraints on such limits. We also show how to compute the finite ‘singularity group’ in the geometric setting.

We introduce in this paper a hypercohomology version of the resonance varieties and obtain some relations to the characteristic varieties of rank one local systems on a smooth quasi-projective complex variety M. A logarithmic resonance variety is also considered and, as an application, we determine the first characteristic variety of the configuration space of n distinct labeled points on an elliptic curve. Finally, for a logarithmic 1-form α on M we investigate the relation between the resonance degree of α and the codimension of the zero set of α on a good compactification of M. This question was inspired by the recent work by Cohen, Denham, Falk and Varchenko.

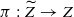Given a normal variety Z, a p-form σ defined on the smooth locus of Z and a resolution of singularities , we study the problem of extending the pull-back 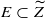π*(σ) over the π-exceptional set . For log canonical pairs and for certain values of p, we show that an extension always exists, possibly with logarithmic poles along E. As a corollary, it is shown that sheaves of reflexive differentials enjoy good pull-back properties. A natural generalization of the well-known Bogomolov–Sommese vanishing theorem to log canonical threefold pairs follows.

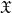Let 𝒱 be a complete discrete valuation ring of unequal characteristic with perfect residue field. Let be a separated smooth formal 𝒱-scheme, 𝒵 be a normal crossing divisor of 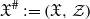, be the induced formal log-scheme over 𝒱 and 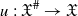be the canonical morphism. Let 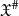X and Z be the special fibers of and 𝒵, T be a divisor of X and ℰ be a log-isocrystal on overconvergent along 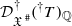T, that is, a coherent left -module, locally projective of finite type over 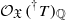. We check the relative duality isomorphism: 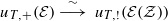. We prove the isomorphism 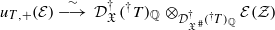, which implies their holonomicity as 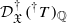-modules. We obtain the canonical morphism ρℰ : uT,+(ℰ)→ℰ(†Z). When ℰ is moreover an isocrystal on overconvergent along T, we prove that ρℰ is an isomorphism.

In a recent paper, Bondarko [Weight structures vs. t-structures; weight filtrations, spectral sequences, and complexes (for motives and in general), Preprint (2007), 0704.4003] defined the notion of weight structure, and proved that the category DMgm(k)of geometrical motives over a perfect field k, as defined and studied by Voevodsky, Suslin and Friedlander [Cycles, transfers, and motivic homology theories, Annals of Mathematics Studies, vol. 143 (Princeton University Press, Princeton, NJ, 2000)], is canonically equipped with such a structure. Building on this result, and under a condition on the weights avoided by the boundary motive [J. Wildeshaus, The boundary motive: definition and basic properties, Compositio Math. 142 (2006), 631–656], we describe a method to construct intrinsically in DMgm(k)a motivic version of interior cohomology of smooth, but possibly non-projective schemes. In a sequel to this work [J. Wildeshaus, On the interior motive of certain Shimura varieties: the case of Hilbert–Blumenthal varieties, Preprint (2009), 0906.4239], this method will be applied to Shimura varieties.

The purpose of this note is to show that the Betti realization of motives is compatible with Grothendieck's six operations and the nearby cycles functors, which in the motivic world, were previously studied by the author. We first review the construction of the Betti realization. Then, we establish some general criteria which, applied to the Betti realization, give the compatibilities we seek except for the one concerning the nearby cycles functors. The latter will be treated in a separate section.

We show that under a suitable transversality condition, the intersection of two rational subtori in an algebraic torus (ℂ*)n is a finite group which can be determined using the torsion part of some associated lattice. We also give applications to the study of characteristic varieties of smooth complex algebraic varieties. As an example we discuss A. Suciu’s line arrangement, the so-called deleted B3-arrangement.

An integer may be represented by a quadratic form over each ring of p-adic integers and over the reals without being represented by this quadratic form over the integers. More generally, such failure of a local-global principle may occur for the representation of one integral quadratic form by another integral quadratic form. We show that many such examples may be accounted for by a Brauer–Manin obstruction for the existence of integral points on schemes defined over the integers. For several types of homogeneous spaces of linear algebraic groups, this obstruction is shown to be the only obstruction to the existence of integral points.