Refine listing
Actions for selected content:
381 results in 14Fxx
Note sur les opérations de Grothendieck et la réalisation de Betti
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 9 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 23 July 2009, pp. 225-263
- Print publication:
- April 2010
-
- Article
- Export citation
A note on the theta characteristics of a compact Riemann surface
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 3 / June 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 415-424
-
- Article
-
- You have access
- Export citation
ON THE INTERSECTION OF RATIONAL TRANSVERSAL SUBTORI
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 86 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 01 April 2009, pp. 221-231
-
- Article
-
- You have access
- Export citation
Brauer–Manin obstruction for integral points of homogeneous spaces and representation by integral quadratic forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 2 / March 2009
- Published online by Cambridge University Press:
- 01 March 2009, pp. 309-363
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
Presque Cp-représentations et (ϕ,Γ)-modules
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 8 / Issue 4 / October 2009
- Published online by Cambridge University Press:
- 30 January 2009, pp. 653-668
- Print publication:
- October 2009
-
- Article
- Export citation
Wild ramification and the characteristic cycle of an ℓ-adic sheaf
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 8 / Issue 4 / October 2009
- Published online by Cambridge University Press:
- 06 January 2009, pp. 769-829
- Print publication:
- October 2009
-
- Article
- Export citation
Semistable reduction for overconvergent F-isocrystals, III: Local semistable reduction at monomial valuations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 1 / January 2009
- Published online by Cambridge University Press:
- 01 January 2009, pp. 143-172
- Print publication:
- January 2009
-
- Article
-
- You have access
- Export citation
Première classe de Stiefel–Whitney des espaces d'applications stables réelles en genre zéro vers une surface convexe
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 8 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 15 December 2008, pp. 383-414
- Print publication:
- April 2009
-
- Article
- Export citation
Réalisation de Hodge du polylogarithme d'un schéma abélien
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 8 / Issue 1 / January 2009
- Published online by Cambridge University Press:
- 20 November 2008, pp. 1-38
- Print publication:
- January 2009
-
- Article
- Export citation
Perverse bundles and Calogero–Moser spaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 6 / November 2008
- Published online by Cambridge University Press:
- 01 November 2008, pp. 1403-1428
- Print publication:
- November 2008
-
- Article
-
- You have access
- Export citation
Differential graded motives: weight complex, weight filtrations and spectral sequences for realizations; Voevodsky versus Hanamura
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 8 / Issue 1 / January 2009
- Published online by Cambridge University Press:
- 16 October 2008, pp. 39-97
- Print publication:
- January 2009
-
- Article
- Export citation
Moduli of toric vector bundles
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 5 / September 2008
- Published online by Cambridge University Press:
- 01 September 2008, pp. 1199-1213
- Print publication:
- September 2008
-
- Article
-
- You have access
- Export citation
Differential equations on complex projective hypersurfaces of low dimension
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 4 / July 2008
- Published online by Cambridge University Press:
- 01 July 2008, pp. 920-932
- Print publication:
- July 2008
-
- Article
-
- You have access
- Export citation
Cohomology of topological groups with applications to the Weil group
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 3 / May 2008
- Published online by Cambridge University Press:
- 01 May 2008, pp. 633-656
- Print publication:
- May 2008
-
- Article
-
- You have access
- Export citation
Semistable reduction for overconvergent F-isocrystals, II: A valuation-theoretic approach
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 3 / May 2008
- Published online by Cambridge University Press:
- 01 May 2008, pp. 657-672
- Print publication:
- May 2008
-
- Article
-
- You have access
- Export citation
Moduli spaces of orthogonal and symplectic bundles over an algebraic curve
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 3 / May 2008
- Published online by Cambridge University Press:
- 01 May 2008, pp. 721-733
- Print publication:
- May 2008
-
- Article
-
- You have access
- Export citation
A Takayama-type extension theorem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 2 / March 2008
- Published online by Cambridge University Press:
- 01 March 2008, pp. 522-540
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
Facteurs epsilon p-adiques
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 2 / March 2008
- Published online by Cambridge University Press:
- 01 March 2008, pp. 439-483
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
On lattices in semi-stable representations: a proof of a conjecture of Breuil
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 1 / January 2008
- Published online by Cambridge University Press:
- 01 January 2008, pp. 61-88
- Print publication:
- January 2008
-
- Article
-
- You have access
- Export citation
Stability conditions for generic K3 categories
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 1 / January 2008
- Published online by Cambridge University Press:
- 01 January 2008, pp. 134-162
- Print publication:
- January 2008
-
- Article
-
- You have access
- Export citation
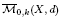 carries different real structures induced by
carries different real structures induced by 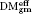 (and give a ‘differential graded enhancement’ of it). This enables us to able to verify that DM
(and give a ‘differential graded enhancement’ of it). This enables us to able to verify that DM (
(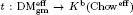 ;
; 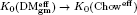 . A motif is mixed Tate whenever its weight complex is. Over finite fields the Beilinson–Parshin conjecture holds if and only if
. A motif is mixed Tate whenever its weight complex is. Over finite fields the Beilinson–Parshin conjecture holds if and only if 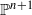 . In this paper we find an effective lower bound for the degree of
. In this paper we find an effective lower bound for the degree of 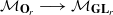 (respectively
(respectively 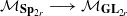 ) from the moduli space of orthogonal (respectively symplectic) bundles to the moduli space of all vector bundles over
) from the moduli space of orthogonal (respectively symplectic) bundles to the moduli space of all vector bundles over 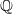 -divisor that has Kawamata log terminal singularities on the submanifold from which extension occurs. In this paper we weaken the positivity assumptions on the twisting line bundle to what we believe to be the minimal positivity hypotheses. The main new idea is an
-divisor that has Kawamata log terminal singularities on the submanifold from which extension occurs. In this paper we weaken the positivity assumptions on the twisting line bundle to what we believe to be the minimal positivity hypotheses. The main new idea is an 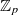 -lattices in semi-stable
-lattices in semi-stable 