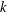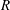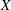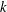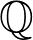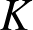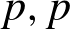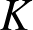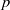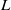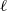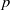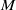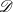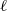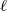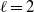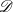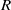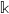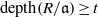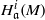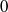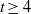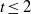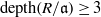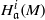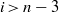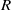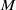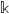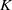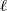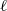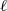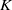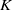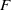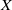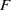Refine listing
Actions for selected content:
378 results in 14Fxx
Noncommutative motives of Azumaya algebras
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 14 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 10 March 2014, pp. 379-403
- Print publication:
- April 2015
-
- Article
- Export citation
MULTIPLICATIVE SUB-HODGE STRUCTURES OF CONJUGATE VARIETIES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 2 / 01 July 2014
- Published online by Cambridge University Press:
- 18 February 2014, e1
-
- Article
-
- You have access
- Open access
- Export citation
Subcategories of singularity categories via tensor actions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 2 / February 2014
- Published online by Cambridge University Press:
- 22 November 2013, pp. 229-272
- Print publication:
- February 2014
-
- Article
- Export citation
Hyperbolicity related problems for complete intersection varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 3 / March 2014
- Published online by Cambridge University Press:
- 18 November 2013, pp. 369-395
- Print publication:
- March 2014
-
- Article
- Export citation
Kummer covers and braid monodromy
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 3 / July 2014
- Published online by Cambridge University Press:
- 17 October 2013, pp. 633-670
- Print publication:
- July 2014
-
- Article
- Export citation
Derived categories and rationality ofconic bundles
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 11 / November 2013
- Published online by Cambridge University Press:
- 07 October 2013, pp. 1789-1817
- Print publication:
- November 2013
-
- Article
- Export citation
A vanishing theorem and symbolic powers of planar point ideals
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 01 October 2013, pp. 373-387
-
- Article
-
- You have access
- Export citation
Trivial zeros of
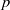 $p$ -adic
$p$ -adic 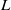 $L$ -functions at near-central points
$L$ -functions at near-central points
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 3 / July 2014
- Published online by Cambridge University Press:
- 24 September 2013, pp. 561-598
- Print publication:
- July 2014
-
- Article
- Export citation
Variants of formal nearby cycles
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 4 / October 2014
- Published online by Cambridge University Press:
- 19 August 2013, pp. 701-752
- Print publication:
- October 2014
-
- Article
- Export citation
Microlocal Euler classes and Hochschild homology
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 3 / July 2014
- Published online by Cambridge University Press:
- 18 July 2013, pp. 487-516
- Print publication:
- July 2014
-
- Article
-
- You have access
- Export citation
Rationality problems and conjectures of Milnor and Bloch–Kato
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 8 / August 2013
- Published online by Cambridge University Press:
- 03 June 2013, pp. 1312-1326
- Print publication:
- August 2013
-
- Article
- Export citation
GENERIC VANISHING THEORY VIA MIXED HODGE MODULES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 1 / 2013
- Published online by Cambridge University Press:
- 17 May 2013, e1
-
- Article
-
- You have access
- Open access
- Export citation
Cohomological and projective dimensions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 7 / July 2013
- Published online by Cambridge University Press:
- 01 May 2013, pp. 1203-1210
- Print publication:
- July 2013
-
- Article
- Export citation
Independence of
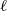 $\ell $-adic Galois representations over function fields
$\ell $-adic Galois representations over function fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 7 / July 2013
- Published online by Cambridge University Press:
- 25 April 2013, pp. 1091-1107
- Print publication:
- July 2013
-
- Article
- Export citation
Depth of
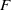 $F$-singularities and base change of relative canonical sheaves
$F$-singularities and base change of relative canonical sheaves
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 05 March 2013, pp. 43-63
- Print publication:
- January 2014
-
- Article
- Export citation
Corrigendum: Varieties with ample cotangent bundle (Compositio Math. 141 (2005), 1445–1459)
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 3 / March 2013
- Published online by Cambridge University Press:
- 28 February 2013, pp. 505-506
- Print publication:
- March 2013
-
- Article
- Export citation
Computing zeta functions of nondegenerate hypersurfaces with few monomials
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 14 February 2013, pp. 9-44
-
- Article
-
- You have access
- Export citation
Hyperplane arrangements of Torelli type
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 2 / February 2013
- Published online by Cambridge University Press:
- 14 December 2012, pp. 309-332
- Print publication:
- February 2013
-
- Article
- Export citation
On the center of the ring of differential operators on a smooth variety over ℤ/pnℤ
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 31 October 2012, pp. 63-80
- Print publication:
- January 2013
-
- Article
- Export citation
A geometric approach to Orlov’s theorem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 5 / September 2012
- Published online by Cambridge University Press:
- 10 July 2012, pp. 1365-1389
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation